割合、比、速さの基礎練習

本記事は我が家で実施した表題の内容の指導方法を御紹介する記事です。

我が家の場合は特別な工夫をせずに愚直に反復練習を致しました。

力技と言いますか、ごく普通のやり方ですね。

以下の記事も参考にしてみて頂けましたら幸いです。

こちらは本記事の続編です。

割合の例で言えば
例えば

• 200円の1％は何円？
• 1％が2円なら100％は何円？
• 2割3分5厘は何％？
• 23.5％は何割何分何厘？
• 1／2は何％？
• 50％を分数で表わすと？
• Ａ：Ｂ＝1：2です。ＡはＢの何％？
• ＡはＢの50％です。Ａ：Ｂは？

このような問題を毎日繰り返し反復学習するだけです。
覚えるまでずっとです。

例えば我が家の場合、記憶力が弱めの息子ですから、３週間以上反復学習をする事もありました。

難しい問題を出す必要はありません。
毎日数字を変えるだけで良いです

同様に速さでしたら以下のように未知数を変えて反復学習します。

• 時速15kmで3時間走ると何km進む？
• 3時間走ると45km進んだ。時速何km？
• 45km先に時速15kmで向かうと何時間？

割合なら・・・・
国語で言う　だから⇔なぜなら　の言い換えと同じように
小数⇔％⇔歩合⇔分数⇔比
の言い換えを反復学習します。

速さなら・・・・
未知数を替えて反復計算
ただひたすら特に工夫もせず反復学習をしているだけです。
毎日反復学習をしていると

1／2は50％
速さ×時間は距離
距離÷速さは時間

このような内容が脳に染み付きます。
毎日反復学習するのがとても大事です。
特別な工夫をしなくても、反復練習するだけで良いと思います。

誤解のないように念の為。工夫しても良いと思いますよ。
以下のような　は、じ、き　の図など。
お子様の好みの方法で暗記して頂ければ良いと思います。

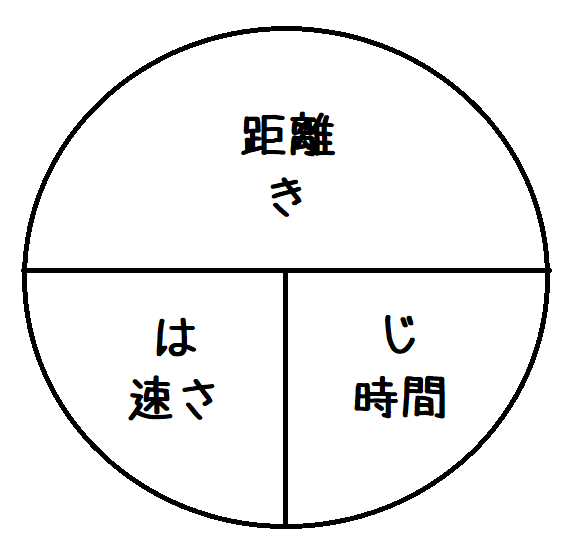
定義を覚えるための暗記作業ですから、どのような方法でも覚える事が出来れば問題ありません。
ただの暗記作業ですからね。

人間が勝手に　速さ×時間＝距離　と定義しただけです。
四則計算が成り立つように
1／2 ＝0.5＝50％
と定義しただけです。
そこに特別な論理はありません。　ただの定義です。

数学で言えば　Ａを自然数とする　と定義した事と同義です。
速さ×時間＝距離とする
と決めただけです。
普段の生活で言えば　青信号は進む！　赤信号は止まれ！
のようなものです。

焦らずしつこく毎日反復練習していれば誰でも身に付くと思います。

我が家の学習事例が少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。

ではまた！