【まとめ】我が家の算数と数学の進捗 小学6年生2月現在

2024.4.7 定期更新
2024.5.5 定期更新
2024.8.9 定期更新
2025.2.15 定期更新
2025.3.3 図の誤記訂正など

本記事は　我が家の学習状況を時系列にまとめた記事　です。

正確な学習記録は付けていないため、多少は時系列のズレがあります事は御承知おき下さい。
学習者（息子）は早生まれの小学6年生　2025年 中学受験組です。
通塾および通信教育は行わず、家庭学習のみで学習を進めてきました。

我が家は楽しい家庭学習を学習方針としています。

また、親子で楽しく学び、共に成長していく事、そして親子で楽しく学習をした思い出を作る事が学習目的の一つです。

学習ルート

補助教材を除くメイン教材の学習ルートは以下の通りです。

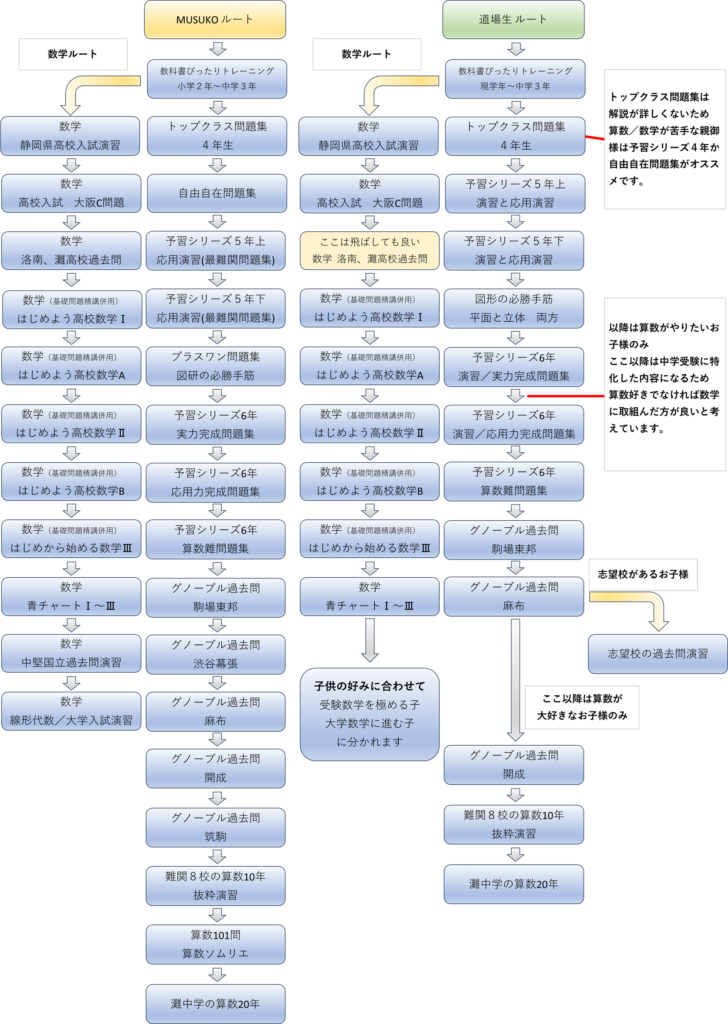
小1-12月　家庭学習開始

メイン教材は教科書ぴったりトレーニング。
小学2年生のぴったりトレーニングから始めました。
副教材としてドリルの王様などの計算ドリルを併用しました。

また、定着のための復習として以下のような自作の問題集を併用しました。毎日の復習として2～4ページの学習を進めました。

小2-7月～

教科書ぴったりトレーニング小４までの範囲学習が終了しました。
数学検定8級【小学4年生レベル】に合格

小2-9月～

教科書ぴったりトレーニング　小学範囲は全て終了しました。この辺りから学習習慣も付き、学習ペースが加速したように思います。
割合や比などの復習も一通り終わり、殆ど間違えない状態まで習熟しました。

小2-10月～

教科書ぴったりトレーニング　中学1年～中学３年を購入し履修を開始しました。
ハイクラスドリル小5から抜粋した問題を自作問題集に書き込むなどして、やや難し目の算数にも取り組みました。

小2-11月～

数学検定5級【中学1年生レベル】に合格
トップクラス問題集小学4年【算数】の学習を開始しました。

またずっと併用して学習している自作問題集ノートがこの時点で１８冊目に達しました。
この自作問題集ノートは最終的に25冊程度まで増え、復習に使い続けました。

小3-4月～

教科書ぴったりトレーニング　中学３年までを終了しました。
数学検定3級【中学3年生レベル】に合格しました。
中学範囲までの範囲学習が一通り完了しました。

小3-5月～

公立高校入試の過去問演習を開始しました。
トップクラス問題集小学4年【算数】を継続学習。
中堅中学の過去問演習を開始しました。
高校数学の学習を開始しました。

小3-7月～

一般的な公立高校入試数学は満点が取れるレベルに達したため、やや難しい大阪Ｃ問題の演習を開始しました。
トップクラス問題集小学４年【算数】を継続学習。

小3-8月～

高校入試・大阪C問題の習熟が進み間違えなくなったため、難関私立高校（灘高校・洛南高校）の入試問題演習を開始しました。
トップクラス問題集小学４年【算数】の学習が復習を含めて完了しました。

小3-9月～

自由自在問題集【算数】の演習を開始しました。

中学受験の定番問題集である予習シリーズ一式を購入し、自由自在問題集との併用学習を開始しました。
予習シリーズは5年生(上)の応用演習問題集（最難関問題集の旧版）から開始しました。
【四谷大塚HP】

数学検定 準2級【高校１年生レベル】に合格しました。

小3-10月～

自由自在問題集【算数】の演習を継続。
予習シリーズ5年(上)の応用演習問題集を終了しました。
数学検定2級取得に向けた学習を開始

小3-11月～

自由自在問題集【算数】の演習を継続。
予習シリーズ5年(下)の応用演習問題集を開始しました。
数学検定2級の学習継続

小3-12月～

自由自在問題集【算数】の演習を継続。
予習シリーズ5年下の応用演習問題集を継続。

小3-1月～

自由自在問題集【算数】が一通り完了し、復習を開始しました。
予習シリーズ5年下の応用演習問題集が一通り終了し復習を開始しました。
図形の必勝手筋平面図形編　立体図形編の学習を開始しました。
はじめよう高校数学を使用し　数学ⅠA・2Bの復習を開始しました。

小3-2月～

プラスワン問題集の学習を開始しました。
図形の必勝手筋を継続学習。
予習シリーズ5年上下　応用演習問題集の復習を継続。
初めから始める数学シリーズの学習を開始しました。（数Ⅲ）

小3-3月～

この頃から英語学習を開始したため、算数／数学の学習ペースがやや低下しました。
プラスワン問題集の学習が終了しました。
図形の必勝手筋　平面図形の習熟が終わり、立体図形を本格的に開始しました。
予習シリーズ5年上下　応用演習問題集の復習を継続。
初めから始める数学シリーズの学習を継続（数Ⅲ）

小4-4月～

図形の必勝手筋　立体図形の学習を継続。
予習シリーズ5年上下　応用演習問題集の復習が終わりました。
予習シリーズ6年上　実力完成問題集の学習を開始しました。
数学検定２級に合格しました。
初めから始める数学シリーズ継続（数Ⅲ）
高校数学　青チャートの学習を開始しました。
復習と定着を兼ねて　センター試験の過去問演習を開始しました。

小4-5月～

図形の必勝手筋　立体図形の学習を継続。
予習シリーズ6年上　実力完成問題集の学習を継続
初めから始める数学シリーズ（数Ⅲ）の学習が一通り終了しました。よって高校数学の教科書レベルの範囲学習が一通り完了しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-6月～

図形の必勝手筋　立体図形の学習を継続。
予習シリーズ6年上　実力完成問題集の学習が終了しました。
予習シリーズ6年上　応用力完成問題集の学習を開始しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-7月～

図形の必勝手筋　立体図形の学習を継続。
予習シリーズ6年上　応用力完成問題集を進めつつ実力完成問題集の復習を継続。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-10月～

図形の必勝手筋　立体図形の学習が終了しました。
予習シリーズ6年上　応用力完成問題集と実力完成問題集の復習が終了しました。
予習シリーズ6年下　入試実践問題集【難関校】の学習を開始しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-11月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
予習シリーズ6年下　入試実践問題集【難関校】の学習が終了しました。
予習シリーズ6年下　算数難問題集の学習を開始しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-12月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
図形は継続しないと幾何の能力が落ちるため、継続しています。
予習シリーズ6年下　算数難問題集の復習が完了しました。予習シリーズ【算数】の学習が全て完了しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-1月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
グノーブル過去問シリーズ　駒場東邦の演習を開始しました。
グノーブル過去問シリーズ　渋幕の演習を開始しました。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-2月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
グノーブル過去問シリーズ　駒場東邦の演習を終了しました。
グノーブル過去問シリーズ　渋谷教育学園幕張中学の演習を継続。
青チャートⅠA・2Bの学習を継続。
センター試験の過去問演習を継続。

小4-3月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
グノーブル過去問シリーズ　渋谷教育学園幕張中学の演習を終了しました。
グノーブル過去問シリーズ　麻布中学の過去問演習を開始しました。
青チャート　数1A～2Bの学習が完了し数Ⅲ中心の学習へ移行しました。
センター試験の過去問演習を継続。

小5-4月～

図形の必勝手筋は幾何の能力を維持するため、定期的な復習を継続。図形に関しては継続的に学習しないと能力が定着しないため、継続的に復習を続けています。
グノーブル過去問シリーズ　麻布中学の過去問演習を終了しました。
グノーブル過去問シリーズ　開成中学の過去問演習を開始しました。
青チャート数Ⅲの学習を継続
センター試験の過去問演習を継続。

小5-5月～

グノーブル過去問シリーズ　開成中学の過去問演習を継続。
青チャート数Ⅲの学習を継続
センター試験の過去問演習を継続。
大学数学を一部履修開始。線形代数・行列など。

小5-6月～

グノーブル過去問シリーズ　開成中学の過去問演習がほぼ終了。あとは多少の復習のみ。
青チャート数Ⅲの学習を継続
センター試験の過去問演習を継続。
大学数学を一部履修開始。線形代数など。

小5-7月～

グノーブル過去問シリーズ　開成中学の過去問演習が復習まで終了。
青チャート数Ⅲの復習
中堅国公立大学の過去問演習、センター過去問演習
大学数学　線形代数の学習

小5-8月～

グノーブル過去問シリーズ　筑駒中学　開始～終了
灘中・開成中・筑駒中受験生なら必ず解いておくべき算数101問　開始
関西　難関8校の過去問　抜粋演習開始
青チャート数Ⅲの復習【継続して少しずつ実施】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続して少しずつ実施】
大学数学　線形代数の学習【継続して少しずつ実施】

小5-9月～

灘中・開成中・筑駒中受験生なら必ず解いておくべき算数101問　終了
関西　難関8校の過去問　抜粋演習【継続】
青チャート数Ⅲの復習【継続して少しずつ実施】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続して少しずつ実施】
大学数学　線形代数の学習【継続して少しずつ実施】

小5-10月～

灘中の過去問20年　開始
関西　難関8校の過去問　抜粋演習　終了
青チャート数Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
大学数学　線形代数の学習【継続】

小5-11月〜

灘中の過去問20年　【継続】
西大和の過去問20年　開始
青チャート数Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
一ツ橋、阪大　数学過去問演習　開始
大学数学　線形代数の学習【継続】

小5-12月〜

灘中の過去問20年　終了
西大和の過去問20年　【継続】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
一ツ橋、阪大　数学過去問演習　【継続】
大学数学　線形代数の学習【継続】

11月から変化無しですが、灘中算数が終わりましたので、やや数学と機械工学の学習を多めにしています。

小5-1月～

西大和の過去問20年　【終了】
東大寺学園中の過去問20年　【開始】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
一ツ橋、阪大　数学過去問演習　【継続】
大学数学　線形代数の学習【継続】

あまり変わり映えがしません。
東大寺の過去問を開始しました。灘で随分鍛えられたのか最初から高得点です。
特に指導無しで一人で進める事が出来ています。
もう算数はあまり指導しなくても大丈夫かもしれません。

一方、数学の論証はまだまだ論理が甘く、指導が必要です。
しかしながら、随分良い論証が書けるようになってきました。

Musukoがコラムを執筆しておりますが、これも楽しみながら国語力、論証力を向上させる良いトレーニングになっています。
小学生にとってブログで長文を書くのは中々大変です。
楽しみながら執筆するMusukoを見ていると「成長したなぁ」と感じます。

小5-2月～

東大寺学園中の過去問20年　【終了】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
一ツ橋、阪大　数学過去問演習　【継続】
大学数学　線形代数の学習【継続】

数学ではありませんが機械工学の学習と実習を多めに実施しています。
また、統計の学習を本格的に始めました。

こちらの書籍で基礎的な内容を学んだ後にいわゆる【赤本】に取組む予定です。

有名な通称【赤本】と呼ばれる統計の入門書です。

統計は全ての方にお勧め出来る学問です。
是非親子で一緒に学んでみて下さいませ。

小5-3月～

灘中学過去問、筑駒中学過去問など難関校の過去問の復習【開始】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
高校数学から始める統計学【開始】
大学数学　線形代数の学習【継続】

さて、算数は難関校の過去問をやりつくしてしまったので灘中、筑駒中の過去問の復習を中心に進めています。
『場合の数』の分野に少しだけ苦手意識があるため、『場合の数』を中心に復習しています。
殆どの場合、解き筋はあっており、数えモレなどのケアレスミスが間違いの原因ですから、ケアレスミス対策をしている感じですね。

数学は一ツ橋と阪大の過去問を解いておりましたが、統計学が楽しくなってきたようでしたので、統計学の学習中心に切り替えています。
青チャート、センター過去問で総復習を実施しつつ、統計学を学んでいる格好です。
機械工学も引き続きノンビリ学んでおります。

小6-4月～

灘中学過去問、筑駒中学過去問など難関校の過去問の復習【継続】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
高校数学から始める統計学【継続】
大学数学　線形代数の学習【継続】

さて、算数は灘中、筑駒中の過去問の復習が終わり、西大和，東大寺，開成あたりを進めています。以前に間違えた問題のみを進めておりますが、殆ど解けており順調です。

統計学は性に合ったようで統計検定2級合格に向けた学習に取組み始めました。
小学生の間に2級は合格出来そうな気がします。

機械工学については読書中心ですが、機械実用便覧を中心に学んでいます。

こちらの書籍が概ね理解出来ていれば、技術士一次試験（機械部門）は合格可能です。
熱力学あたりがちょっとハードルが高いので小学生の間に合格は厳しいかな。。。

一次試験の最年少合格者は小学3年生のようですが、とんでもないですね。
少なくとも高校数学レベルは理解していないと厳しいはずですが、小学３年とは驚きました。

我が家の６年生はこんな感じで学習を進めています。

小6-5月～7月

算数は正直なところ、新規でやる事はなくなりました。

灘中過去問 ⇒ 筑駒過去問 ⇒ 開成過去問 ⇒ 西大和過去問
の順番でループしています。

灘中の過去問では制限時間が半分程度で処理出来るようになりました。
開成、筑駒などでも随分時間が余るようになり、処理速度の向上が観られます。

という事で、算数は過去問演習をする程度で数学～機械工学を中心に学習を進めています。

灘中学過去問、筑駒中学過去問など難関校の過去問の復習【継続】
青チャート数Ⅰ～Ⅲの復習【継続】
カルキュール数学計算演習【毎日継続】
中堅国公立大学の過去問演習、センター過去問演習【継続】
高校数学から始める統計学【継続】
機械工学便覧、機械設計便覧、機械実用便覧の学習【継続】

さて、統計学は統計検定2級の過去問で合格点を取れるようになりましたので、そのうち受験予定です。

高校数学については中堅～難関私大（GMARCHレベル）ならば合格者平均以上は取れるのではないかと思います。
難関国立の二次試験レベルでも随分戦えるようになってきました。
6年生になり、記述能力の向上がみられます。この数学を通じて得た、記述能力は国語の記述問題にも活かされているように感じます。
「要約して、読み手が理解出来るように説明する」という点では数学と国語は通ずるところがあるのかと考えております。

機械工学については数学、物理系を中心に学んでいます。
例えば３次元座標計算（行列）や微分方程式を用いた応力解析などです。

その他はフーリエ変換による周波数解析、モード解析等々を実施しています。
幸い家にFFT解析可能なインパルスハンマーFFT装置（OROS）が御座いますので、一緒にハンマリング試験などを実施して遊んだりしています。二度打ち条件の分析など大学で学ぶレベルの内容も指導しています。

まぁ世の中広いですが、OROSを使ってFFT解析をしている小学生はさすがに殆どいないでしょう（笑）
本人は楽しそうに取り組んでおりますので良しとしております。

小6-8月～11月

夏休みに入りましたので数学の学習に取れる時間が増加しました。
Sharari-manが海外出張が増加しましたので、以前ほど観てやる事が出来ませんでしたが、コツコツと数学を進めていたようです。

算数については『能力維持』が主目的となりますので、相変わらず過去問のループをしておりました。

灘中過去問 ⇒ 筑駒過去問 ⇒ 開成過去問 ⇒ 西大和過去問
の順番でループをしておりましたが、これらの中学の過去問が解けるレベルになってからは、これらの過去問演習を続けていれば、充分な能力維持が出来ると考えております。

灘中、筑駒中の過去問演習では中学受験算数を解くために必要なエッセンスが十二分に詰め込まれています。
難易度、時間の厳しさについてもトップクラスですから、この２つの中学過去問で安定して高得点が取れるようでしたら、どこの中学の問題でも高得点が狙えるでしょう。

さて、算数以外の数学関連学習については以下の通りです。

■青チャート数Ⅰ～Ⅲの復習【継続】
青チャートについては随分理解が進みましたが、やはり継続してやらないと忘れていきます。
よってコツコツ継続的に学習を続け能力の維持・向上を図っています。
■カルキュール数学計算演習【毎日継続】
カルキュール計算演習は本当に丁度良い難易度です。
難し過ぎず、簡単過ぎない。朝晩の計算演習として活用しています。
■中堅国公立大学の過去問演習、センター過去問演習【継続】
静岡大学、福井大学、金沢大学などの中堅国立の数学については概ね解けるようになったでしょうか。
時間的にも余裕がありますが、まだ少し論証が甘い状態ですので改善が必要です。
■機械工学便覧、機械設計便覧、機械実用便覧の学習【継続】
機械工学については上記以外に以下の専門書を用いて、専門的な学習も少しずつ進めています。
☆モード解析入門（長松昭男）
高校数学レベルから丁寧に『振動』を扱うための学習をする事が出来る良書です。
高校数学を一通り履修している方でしたら読む事が出来ます。
インパルスハンマによる振動解析など実践的な内容を学ぶ事が出来ます。
我が家ではこちらの書籍を利用してMusukoに振動解析の手法を学ばせています。
☆工作機械の形状創成理論（稲崎一郎）
稲崎先生の名著、形状創成理論です。
こちらは数学を実践的に利用した、工作機械における座標計算の手法を学べる良書です。
座標計算というカテゴリーはロボットの自律制御など応用範囲が多岐に渡りますから非常にオススメ出来る分野です。
こちらは高校数学～一部大学数学までが範囲となりますが、高校数学を一通り履修している方でしたらそれなりに読む事が可能と思います。

さて、統計学は統計検定2級の学習を継続しつつ、実践的な内容について学んでいます。
実戦的な内容とは例えば機械の評価です。
例えば自身で設計した機械の評価計画をするにあたり、どれくらいの回数評価すれば有効な評価と言えるのか？
それらを統計的に分析し、評価計画を立てる業務です。

このような感じで算数／数学の学習を進めております。

数学者を志す方以外の多くの方にとっては『数学は何かをするためのツール』であるはずです。
上述したような実践的な数学利用方法を学ぶ事は数学を学ぶ上で大変役に立ちますし、興味を持つための良い手法です。

何に使うか良く分からないけれど、とにかく三角関数、微積、極限を丸暗記しよう！
という状態は興味を持ちづらく、公式や解法を暗記するという作業になりがちです。
受験生でしたらある程度仕方ないように思いますが、先取り学習という余裕のある状況の我が家では『実践的な内容を並行して学び、理解を深め、より興味が持てるような活動をする。』という活動を重視しております。

読者様で先取り学習を進めている方も是非、『受験』というカテゴリーにだけに囚われず、実践的で楽しい家庭学習に取組んで頂ければと思います。

小6-12月～2月（受験直前期）

さて、1月からは関西受験、2月は関東受験と受験が迫ってまいりましたので、12月からは受験対策の学習を優先して進めました。

そのため、数学や機械工学の学習はやや少なくなりました。とはいえ、能力維持のための計算演習などには継続して取り組みました。

算数については上述した４校の過去問ループに加え、受験予定校の過去問にも取り組みました。
関西、関東合わせて5校ほど受験予定でしたので、それらの過去問に取り組んだ感じです。

算数の能力については浮き沈み無く、スランプも無く、安定して高得点を取る事が出来る状態です。
よって、直前期は算数は過去問演習を毎日1～2年分やる程度にとどめ、国理社の暗記学習を中心に進めておりました。

算数／数学の先取り学習を進めていた故に直前期に焦らず、国理社の暗記学習に時間を割く事が出来たと言えると思います。

本番までずっとこのようなペースでマイペースに学習を進めておりました。

■本番での出来栄え
算数については全ての受験校で合格者平均点は上回る出来栄えだったと思います。
具体的には全問時間内に解く事が出来て、見直し時間も充分に取れた。という状態です。
得点開示のある学校では95%程度の得点率でした。

本番で緊張せずに実力を発揮出来たという事ですね。
家庭学習中心で模試の少ない我が家では本番での緊張だけが唯一の懸案事項でしたが、杞憂に終わったようです。

Musukoはテストでは緊張しないタイプです。
学校での発表など人前で話をする時は緊張しているように思いますが、テストは大丈夫なようです。

本人から報告もありましたが無事に志望校に合格出来たようで大変喜んでおりました。
これからも楽しく学び続けていってもらえれば大変嬉しく思います。

算数／数学の能力目安【2025年2月現在】

過去問演習は家でリラックスした状態で解いているため、本番で同様の得点が出来るとは考えておりません。
参考値とお考え下さい。

さて、算数の能力については最後の報告になりますね。
以下のような能力で本番を迎えました。

• 灘中学　過去問　正答率　96.2%（約20年分　平均して時間は10～15分余り）
• 筑駒中学　過去問　正答率　97.4％（約20年分　平均して時間は10分余り）
• 開成中学　過去問　正答率　95.6%（約20年分　平均して時間は15～20分余り）
• 西大和中学　過去問　正答率　96.8%（約20年分　平均して時間は15～20分余り）
  ※複数回実施した過去問演習の最後の20年分です。
  　当然一度解いた事がある問題ですが、随分前ですので忘れてしまうというのが実情です『こんな問題あったなぁ』くらいには覚えていると思いますが。
  
  解けない問題は無く、間違いは全て単純な計算ミス、勘違い等です。
  Musukoの特性上これらを完璧にゼロにするのは難しいように思いますので、『出来るだけ減らす』『解けない問題を無くす』という方針で指導しておりました。

以下はいつも掲載しておりました、過去問1周目の得点率です。
御参考までに残しておきます。

• 芝・本郷中学　正答率　95%～
• 駒場東邦中学　正答率　94.2％
• 渋幕　正答率　89.6％
• 麻布　正答率　87.9％
• 開成　正答率　87.6％
• 筑駒　正答率　89.6%
• 灘　　正答率　約83%
• 西大和　正答率　約92%
• 東大寺　正答率　約92%
• 算数101問　正答率 88.1％
  
• 公立高校入試　正答率95%前後(演習が進んだ後)
• 公立高校入試（大阪C問題）正答率90％前後(演習が進んだ後)
• センター試験（数1A 2B）　　正答率90%以上(演習が進んだ後)
• 数学検定２級合格（以降は取得出来ていないのではなく、本人の気分が乗らないため、受験していません）
• 地方国公立二次試験　合格者平均以上（演習が進んだ後）
• 中堅国公立二次試験　合格者平均以上（演習が進んだ後）

学習スケジュール

小学4年～6年の学習スケジュールです。御参考までに。

我が家の学習方針

学習の目的は　社会貢献をしながら面白可笑しく生きるための能力を身に付ける事。
小学、中学、高校、大学、社会のカテゴリーは気にせず、必要な事を学ぶ。
親子で楽しく家庭学習に取組み共に成長する。

いつも笑顔で楽しく学ぶ。

少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。

ではまた！