2025.3.25 パターン⑤を追加
さて、本記事は掛算の計算手順に関する事を記載した記事です。
我が家と算数道場で指導している方法を参考に御紹介させて頂きます。
私は暗算、ソロバンのプロではないので最適解では無いかもしれない事は御承知おき下さい。
しかしながら、長年生きてきて、このレベルの暗算速度があれば困った事はないので、このレベルまで習熟する事を目安に息子や生徒に指導しております。
基本はパターン①かパターン②で計算をします。
パターン③と④も教えていますが、生徒達が使うかどうかは好み次第です。
そろばん経験者はパターン⑤も良いでしょう。慣れるとかなり早いです。
Sharari-manもパターン⑤で計算するケースが多い事に気が付きましたので追加致しました。
2桁×1桁の掛け算
パターン①
ごく一般的な方法です。
10の位を先に計算します。
18×4=40 + 32 = 72
パターン②
1の位が1,2,8,9 の場合は繰り上がり、繰り下がりが発生しないため計算が早くなります。
(20-2)×4= 80 – 8 = 72
この計算手法は2桁×2桁でも使います。
2桁×2桁の掛け算
パターン①
ごく一般的な方法です。
10の位を先に計算します。
46×34=46×30 + 46×4 = 1380 + 184 = 1564
パターン⓶
50に近い数字はこの方法を使用した方が計算が早くなります。
46×34 = (50-4) ×34 = (1700 – 136 ) = 1564
パターン③
数学で学ぶ 因数分解 を利用した有名な計算方法です。
46×34 = 1200 + 340 + 24 = 1564
1200は 40 × 30
340は (4×4+6×3)×10
24は 6×4
有名な方法です。システマチックに解けます。
(40 + 6)×(30 +4)に因数分解して
40×30 + ( 40×4 + 30×6 ) +24 しているだけです。
パターン④
③と同じ因数分解を利用した手法の引き算パターン。
46×34 = (50 – 4)×(40-6) と考える
2000 – 300 – 160 + 24 = 1564
パターン⑤
そろばん経験者はこちらの手法で計算すると思います。
46×34
46×3=138
4×4=16
138+16=154 ⇒ 1540
6×4=24
1540+24=1564
上の位から順に処理していく方法です。
かなりシステマチックに処理出来るため、慣れると早いです。
パターン⑤の解説

2乗の計算
93×93=(100-7)^2
と考えて計算する手法です。
10000 – 1400 + 49 = 8649
73×73=(70+3)^2
=4900+420+9=5329
パターン①での計算と比較すると
73×70+73×3 =5110+219=5329
こちらは2桁×1桁の処理が2回入り計算が長くなります。
一方、上の方法は1桁×1桁を3回計算するだけですから、計算処理量が減っている事が分かると思います。
この計算方法は以下のように場合分けがありまして、1の位に応じてやり方を変えると早いです。
A:1桁目が5未満の場合
1の位と10の位を足し算に分けて計算する。
73×73 = (70+3)^2
B:1桁目が5の場合
以下のように計算する。
75×75 = (70+5)^2= 4900+700 + 25
更に高速に計算する手法があります。
2×5が10になるため、脳内で
(7×7+7=7×8)×100+5^2 = 5600 +25 =5625
と考える事で慣れれば1~2秒程度で答えが出せます。
65×65なら
(6X7)×100 +5^2 = 4225
C:1桁目が5を超える場合
繰り上げをしてそこから引き算で立式し計算する
77×77 = (80-3)^2 と考える。
(80-3)^2 = 6400 – 480 +9 = 5929
掛け算は 2桁×2桁までの暗算が出来れば 殆ど困る事はないと思います
まずは 37 × 6 などの処理からです。
見た瞬間に 180 + 42 と脳内に浮かべば完璧です。
あとは 脳内メモリに 180 と 42 を残したまま 足し算が出来るかどうかです。
これは訓練するしかないですかね![]()
脳のメモリを拡張する作業です。
恐らく個人によって違うと思いますが Sharari-manの場合は
脳内に 180 + 42 という数字が浮かんでいます。
脳内のメモ用紙に 180 + 42 と書いている感じ。
例えば以下の計算でも脳内に 1380 + 184 が浮かんでいます。
46×34=46×30 + 46×4 = 1380 + 184 = 1564
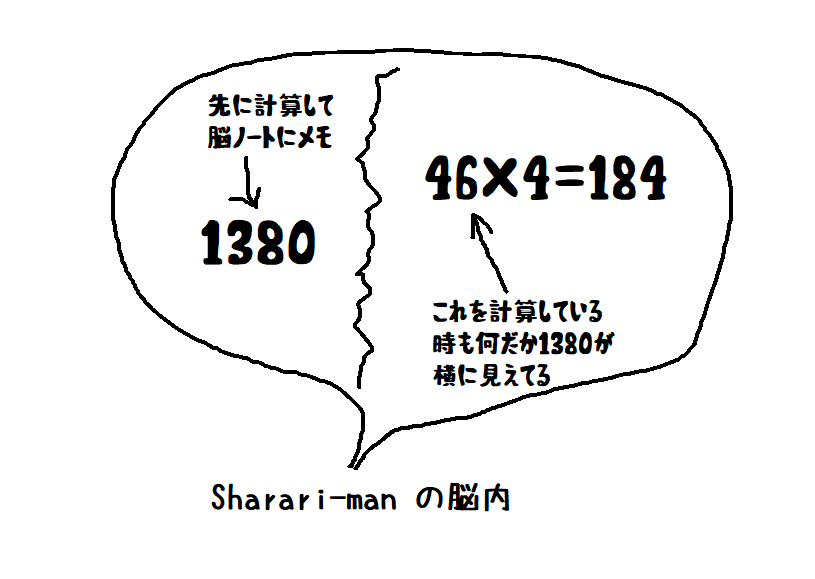
上の画像のようなイメージです。
この絵が脳内に浮かんでいるようなイメージです。
ソロバンは脳内にソロバン画像
将棋棋士は脳内に盤面画像
サッカー選手は脳内にフィールドの鳥観図
技術者は脳内に機械の構造図
このように訓練すれば多くの方が脳内に何らかの画像メモが作れるはずです。
脳内メモリの拡張をするためにも暗算の訓練は良いと思います。
関連記事


我が家の学習事例が少しでも家庭学習に取組む皆様の御参考に望外の喜びです。
ではまた!

コメント【コメント非公開、メールでの返信を御希望される方はその旨をご記入下さい】
コメント一覧 (2件)
Sharari-man様
こんにちは。計算方法の詳細検討、興味深いですね。
私はそろばん経験者なので脳内にそろばんが浮かびます。小3までの経験ですが、濃厚に行っていたためかなりしっかりと根付いています。
私の2ケタx2ケタはパターン⑤の変形で、下の位から計算します。(本来のそろばんの計算方法とは異なります。)
☆46x34
46x4=184
その結果に、1ケタずらして
46x3=138をたす。(そろばん上は1380)
たすといってもそのままたすのではなくて、
184とおいてあるそろばんに、
まず3x4=12を百の位にあわせてたす。→結果1384
一ケタ下にずらして3x6=18をたす。(脳内でそろばんを動かしているだけです。)
1384+180=1564
おそらく自己流ですが、この方が、ケタを間違えづらいためこうしているのかと思います。
☆2乗の計算
77x77
まずは70x70で4900を脳内のそろばんにおく。
次に7x7=49をそろばんにおく。
そうすると、そろばんには4949が置かれる状態になります。次に、
百の位と十の位に、
70x7=49を2回たして(490+490です。490x2の計算はしません。)5929。(10X+Y)2^=10X2^+Y2^+20XYの20XYを、XxYを10の位を基準に2回たすことを行っています。
この利点は、
すべて2ケタ以下の足し算のみ。
九九の計算の結果のみを使用している。
計算ミスを防ぐために自己流で行っているのだと思います。
ご参考までに。
また楽しい記事を、宜しくお願いいたします。
ぞうさん様
いつもコメントありがとう御座います。
返信が遅くなり申し訳御座いません。
計算手法の御提示、大変参考になります。
下の位から計算していく手法は仰る通り、桁数間違いが軽減出来そうです。
後日、記事を修正して追加させて頂こうと思います。
仲間内で効率の良い計算手法について議論する事がありますが、意外と個々でノウハウを持っていて、面白いものだなぁと感じます。
現在、インド滞在時限定でインドスタッフの子供達に算数/数学を指導していますが、彼らはインド式と呼ばれる計算を身に付けており、異常に計算が早いです。
Sharari-manよりも圧倒的に計算速度が速く驚かされますね。
1×1~19×19までを九九のように暗記しているのは有名ですが、その他にも特殊な計算手法を色々と身に付けています。
インドの子供達も可愛く、楽しく学ばせて頂いております。
現地法人の業務が忙しく、中々日本に帰らせてもらえず、道場生の指導が滞るのが悩みですね(笑)
コメントありがとう御座いました!
ではまた!