2025.6.8 旅人算、整数、公約数など追加
2025.6.9 流水算、 追加
2025.6.10 仕事算、ニュートン算 追加,誤記訂正など
2025.6.17 差集め算、過不足算、整数 追加
2025.11.9 加筆修正
さて、表題の件です。
本記事では特殊算と数学の関係性について記載してみようと思います。
読者様から問い合わせがあった内容に関するアンサー記事として投稿させて頂いております。
 Sharari-man
Sharari-manそもそも算数の内容は数学に包括されているはずですが、受験算数は算数の知識のみで効率良く解くための特殊な技法を使用する事があります。
とはいえ数学的に解けない訳ではありません。立式の仕方を工夫するなどすれば数学的に効率的に解く事も可能です。
 Sharari-man
Sharari-manあまり算数/数学と分けて考えずに解きやすい方法で楽しみながら解けば良いのではないかと考えております。
私の知る限り難関中学においては数学的解法,例えば連立方程式などを用いても減点されるというような事は聞いておりません。
はじめに
中学受験算数を特別視している方が多くいらっしゃるかもしれませんが、特段数学とやっている事は変わりません。
『どうすれば効率良く処理出来るか?』
を考える事に特化したものが受験算数、一般化し汎用性を高めたものが数学的である と言っても良いでしょうか。
しかしながら数学の世界でも『どうしたら効率良く処理出来るか?』を考える事は重要ですから、数学は何も工夫をしなくて良い訳ではありません。
誤解の無いように言いますが、当然数学の方が受験算数よりも圧倒的に工夫が凝らされたものです。
数学者達の弛まぬ研鑽により磨き続けてきたものですからね。
さて、では受験算数(特殊算)というものは、どういった工夫を凝らしているのかを見てみましょう。
消去算
りんごを3個、みかんを5個買うと490円です。
りんごを4個、みかんを3個買うと470円です。
りんごとみかんは1個あたり何円でしょう。
■消去算
3りんご+5みかん=490円
4りんご+ 3みかん=470円
これは分かり易く、数学で言うところの連立方程式そのものです。
X,Yなどの記号を使わないだけで同じものです。
9りんご+15みかん=490×3=1470
20りんご+15みかん=470×5=2350
11りんご=880円
1りんご=80円
1みかん=50円
つるかめ算①
算数的解法(特殊算)
つるとかめが合計で100匹います。
足の数の合計が280本の時、つるとかめはそれぞれ何匹でしょう?
つるは足が2本
かめは足が4本
かめが一匹増える毎に足が2本ずつ増えます。
全部つるだったとしたら・・・・?
と考えると つる×100匹=足200本
つる99匹 + かめ1匹 だと 99×2本+1×4本=202本
かめが1匹増える毎に2本ずつ増えています。
問題は280本ですから、全部つるだと仮定すると 280-200=80で80本足りません。
足りない分がかめですから、80÷2=40
よって かめは40匹 つるは60匹 となります。
数学的解法①
つるをX匹 かめをY匹とすれば
X+Y=100
2X+4Y=280
連立して
2Y=80
Y=40
X=60
よって かめは40匹 つるは60匹
数学的解法②
こちらが本筋です。
特殊算であろうと、数学であろうと、『効率良く計算するためには?』と考える事は同じです。
つるをX匹 かめをY匹とすれば
全部つるの場合
200本
かめが増えれば2本ずつ増えるのだから
200+2Y=280 という式が立てられます。
よって Y=40、X=60
 Sharari-man
Sharari-manこれが代表例ですが、数学と受験算数に明確な区切りはありません。
数学で効率良く計算するための式を立てれば特殊算風になります。
 Sharari-man
Sharari-manよって受験算数を通じて『効率良く計算するための手法や考え方を学ぶ』というのが受験算数の学び方の本質だと考えています。
つるかめ算②
A問題は5点、B問題は10点、C問題は12点のテストを実施した。
8問に正解し得点は合計69点でした。
A問題とB問題の正答数は同じだった。C問題は何題解けたでしょう?
算数的解法
「面積図を書いて下部分を取り除きましょう」という手法が一般的でしょう。
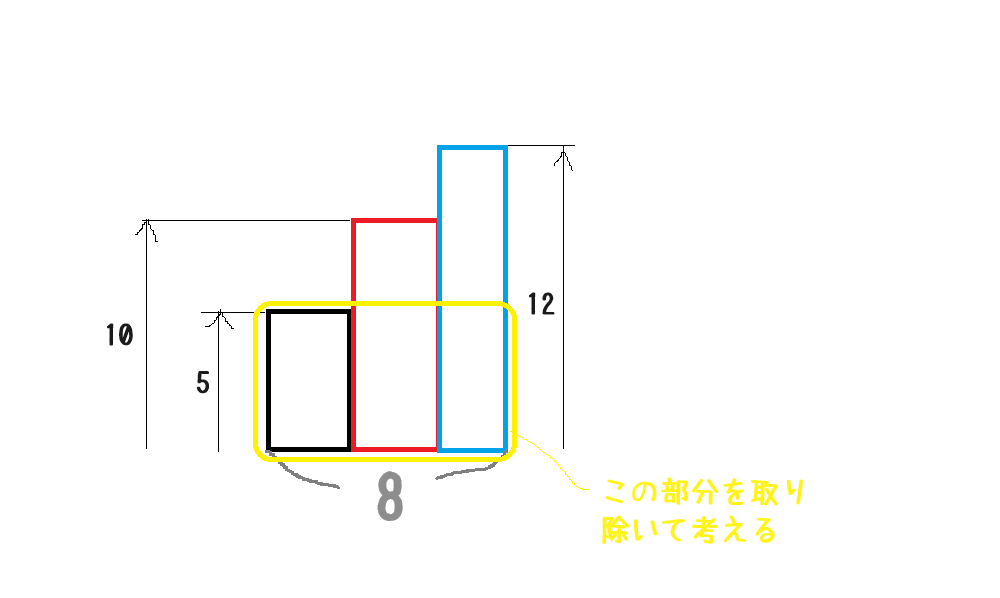
8×5=40点 を合計点である69点から取り除きます。
69-40=29点
下部を取り除いた事でB問題とC問題の得点は以下のように変化します。
B問題:10点⇒5点
C問題:12点⇒7点
5点と7点を使って29点を作れば良い。
あとは数字を当てはめて計算してみれば ・・・
5×3+7×2=29点 となる事が分かる。
よって
A問題3問
B問題3問
C問題2問
C問題は2問正解した が解となります。
数学的解法
AとBの正答数をX Cの正答数をYとすれば以下の式が成り立ちます。
5X + 10X +12Y =69
15X + 12Y = 69
両辺を3で割ると
5X +4Y = 23
適当な数字を代入し
X=3 Y=2
数が大きい場合などは ユークリッドの互除法を使う方法が一般的でしょうか。
XYの係数が互いに素かどうかが重要です。
不定方程式①
97X + 73Y =2404 となる 正の整数 X,Yの組を求めよ。
以下の手法で割とシステマチックに求められます。
73(X+Y)+24X =2404
X+Y=aとすれば
73a +24X=2404
24(X+3a)+a=2404
X+3a=bとすれば
24b +a =2404
特殊解として a=4 b=100
よって
X=88、Y=-84
よって
97(88-X)=73(Y+84)
97と73は互いに素だから
kを整数とすれば
88-X=73k ⇒ X=88-73k
Y+84=97k ⇒ Y=97k -84
算数の場合は X,Yは正の整数だから
k=1 よって X=15、Y=13
不定方程式②
不定方程式の解き方は色々ありますが、算数の範囲では以下の手法で必ず答えを見つける事が出来ます。
灘中学2008 1日目大問2⃣より引用
1個66円のかきと1個35円のみかんを合わせて3890円分買った。このとき,かきは ① 個,みかんは ② 個である。
引用終わり
かきの個数をX みかんをYとすれば
66X + 35Y =3890
右辺の1の位が0のため
Xは5の倍数、Yは2の倍数が確定します。
ゆえに
X=5m 、Y=2n とすれば
330m + 70n=3890
33m + 7n =389
全体を7で割った余りをみると
mを7で割った余りをkとすれば
33m≡-2×k (mod7)
7n≡0(mod7)
389≡4(mod7)
ゆえに
-2k≡4(mod7)
よって k≡-2
よって mは7で割って5余る整数だから
5、12、19、26‥‥
m=12では389を超えるため、mは5で確定
よって m=5、n=32
X=5m=25
Y=2n=64
よって かきは25個、みかんは64個
さて、こちらも①の方法で試しに解いてみましょう。
66X + 35Y =3890
35(X+Y)+31X =3890
X+Y=aとして
35a+31X=3890
31( a + X )+4a=3890
a+X=b とすれば
31b+4a =3890
bが10の倍数であたりをつけて
b=110の時 3410+4a=3890
480=4a a=120
よって 特殊解は a=120、b=110
a + X = b より X=-10
X + Y =a より Y=130
66(X+10)=35(130-Y)
66と35は互いに素ゆえ
X+10 =35k ⇒ X=35k -10
130-Y=66k ⇒Y= 130-66k
算数の場合、XとYは正の整数しかありえないので k=1
よって X=25、Y=64
他にも色々なやり方がありますので、気が向いたら追加しておきます。
いもづる算
Aは1個83円、Bは1個130円、Cは1個200円です。
いくつかずつ購入すると合計金額は4249円になりました。
Aの個数がCの個数の11倍であるとき、Bを何個購入したか答えなさい。
算数的解法
合計金額が4249円です。1の位に注目します。
1の位の数字が9です。BとCでは1の位の9を作れません。
よってAで1の位の9を作ります。
Aの1の位が3ですから
3×3=9しかなさそうです。
またAはCの11倍という事から11の倍数です。
すると Aは3×11に限定されます。
ゆえに Aは33個、Cは3個
4249-(83×33)-(200×3)=910
910/130=7
よってB=7個
数学的解法
Cの個数をX Bの個数をYとします。
Aの個数は条件より11X
83×11X+130Y + 200X =4249
1113X+130Y=4249
1の位を見ればXは3以外ありえません。
ゆえにX=3,Y=7
とくに数学と受験算数で考え方も手法も変わらないように思います。
差集め算①(基本)
個々の差に注目して解く手法です。
1個180円のドーナツと1個200円のパンを合計20個買いました。
間違えてドーナツとパンの個数を予定と反対に買ってしまいました。
すると合計金額が予定より200円安くなりました。
ドーナツとパンをいくつずつ買ったでしょうか?
算数的解法
恐らく塾では線分図を書くように指導されると思いますが、Sharari-manは言葉のみです。
ドーナツとパンの価格の『差』に注目する。
200-180=20 よって差は20円
200円安くなった という事は
200÷20=10 よりドーナツとパンの個数の差は10個です。
少し実験をしてみます。
『合計20個だから』・‥‥
予定していた パンを4個としたら ドーナツは16個
反対にしたら パン16個 ドーナツ4個
差が12個になっちゃうから違う。この差が10個になれば良いから・‥‥
『パン5個とドーナツ15個しかなさそうだ!』
答えは ドーナツ15個 パン5個
数学的解法
予定していたドーナツの個数をX
予定していだパンの個数をY
とおく。
X+Y=20‥‥①
180X+200Y -200=200X+180Y
-20X + 20Y = 200
-X+Y=10‥‥②
①と②を連立して
2X=10
X=5 よって Y=15
答えは ドーナツ15個、パン5個
【別解】
差に注目して ②式を直接的に立式しても良い。
200円安くなったという事はXとYの個数の差が10個だという事だから‥‥
Y-X=10 ‥‥②
差集め算の式の立て方はこちらよりですね。
この手の問題は割とシンプルな問題が多く、立式すれば容易なことが殆どです。
過不足算(難関レベル)
灘中学2017年 一日目 大問2より引用
あるクラスの生徒40人に鉛筆を配ることにしました。男子に5本ずつ,女子に3本ずつ配ると6本余ることが分かりました。そこで,新たに20本を追加して,男子に4本ずつ,女子に5本ずつ配ると,過不足はありませんでした。はじめに用意していた鉛筆は全部で□本です。
引用終わり
数学的解法
この手の問題は過去問解答においても『算数的』と言いつつ、 5男+3女 のように立式している解法が多いように思います。
素直に立式して解けば良いと思いますので数学的解法のみです。
鉛筆の個数をK個
男子の人数をX人
女子の人数をY人
とおく。
X+Y=40‥‥①
5X+3Y+6=K‥‥②
4X+5Y-20=K‥‥③
②と③を連立すれば
X-2Y=-26‥‥④
①と④を連立すれば
3Y=66
よってY=22 だから X=18
②にXとYを代入して
K=5×18+3×22+6=162
よって最初に用意していた鉛筆は 162本
弁償算
つるかめ算と殆ど同じです。
勝利すると5点、負けると-3点、10戦して18点あった場合、何勝何敗ですか?
全勝すると50点、負ける毎に-5-3= -8点
勝ちをX 負けをYとすれば
50-8Y=18
X+Y=10
Y=4
X=6
よって6勝4敗
特殊算の計算の流れで数学的に処理するだけです。
てんびん算(濃度算)
4%100gの食塩水と7%で200gの食塩水を混ぜると何%の食塩水になるでしょうか?
てんびん算とは以下のような図を書いてシステマチックに答えを求める手法です。
比を用いて計算処理するため、面倒な食塩量の算出をする事無く、簡単に濃度を求める事が可能です。
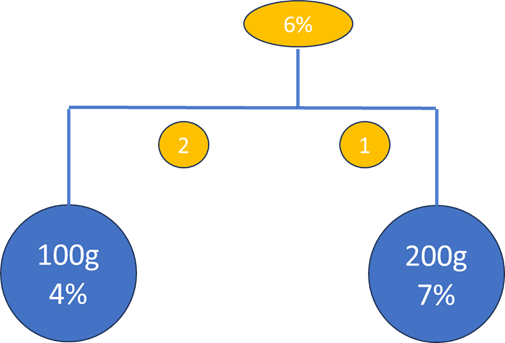
さて、これはどのような仕組みなのでしょうか?
100gと200g の質量比は1:2です。
濃度の比は4:7です。
食塩の量は 質量と濃度をかけたものですから
食塩の質量比は 4×1:7×2=4:14になります。
これを質量で割ったものが濃度ですから
食塩の質量合計は4+14=18
食塩水の質量合計は1+2=3
よって食塩水の濃度は18/3=6
よって6%
数学的解法
混ぜ合わせた後の食塩水の濃度をX%とおく。
質量比は1:2
濃度比は4:7
混ぜ合わせた物の濃度は
X=(1×4+2×7)/(1+2)=6
ゆえに6%
とまぁ、文字式を導入しただけで殆ど同じです。
比で工夫して計算処理しているだけですからね。
平均算
テストを数回受けたところ1~10回目までの平均点が70点
残りのテストの平均点は90点
全てのテストの平均点は80点でした。
テストは合計で何回受けたでしょう?
算数的解法
割愛しますが、面積図を使う方法を指導する塾が多いでしょう。
予習シリーズでも面積図を使う方法で解説されている事が多いです。
数学的解法
テストを受けた合計回数をXとする。
全てのテストの合計点は 80X
1~10回目の合計点は700点
10回目以降のテストの合計点は 90×(X-10)
よって
80X=700+90X-900
200=10X
X=20
よってテストは20回受けた。
指導する際は面積図を書く事もありますが、目的は正しく、効率良く計算出来るように立式する事です。
面積図を上手に書く訓練をする事は特になく、正しく問題文の意味を理解し、立式出来ていれば良いでしょう。
和差算
カードが10枚あります。
カードの片方の面には1,3,5,7,9,11,13,15,17,19 の奇数が書かれています。
もう片方の面には偶数が書かれており、裏表の数を足すと21になります。
例)19のカードの裏側は2
1)今10枚のカードを並べたところ、表側の数の合計は115でした。
カードを1枚ひっくり返すと130になりました。
ひっくり返したカードの表と裏の数字を答えなさい。
算数的解法
裏表を足すと21、ひっくり返すと15増えたので差が15
線分図を書くと‥‥
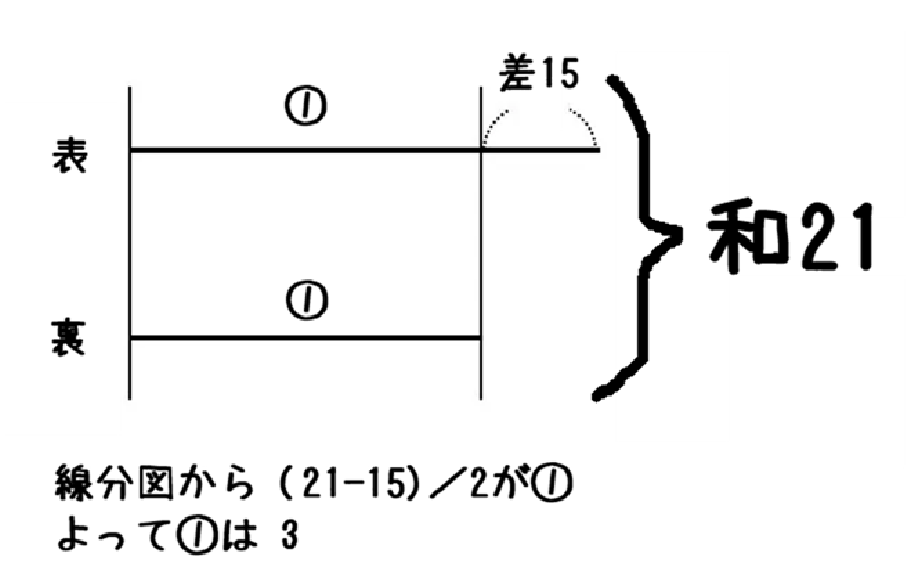
よって答えは3,18
数学的解法
表の数をX、裏の数をYとする。
X+Y=21
YーX=15
連立して 2X=6、X=3
よって 3、18
線分図を書かないだけで、やっている事は同じです。
和差算は難関中学では不定方程式と良くからませてきます。
不定方程式が出てきたタイミングで 不定方程式の解法、例えばユークリッドの互除法などを教えています。
特殊解を見つけ、 X=2k+3 (kは整数)などのように解を見つける手法も教えます。
旅人算①
基礎的な旅人算です。
A点とB点は1000m離れています。
太郎君はA点からB点に向かって歩きます。
次郎君はB点からA点に向かって歩きます。
太郎君は分速100mで歩きます。次郎君が歩く速さは分かりません。
太郎君がA点を出発してから4分後に次郎君と出会いました。
次郎君の歩く速さを求めなさい。
算数的解法
図を書いて整理します。
算数、数学どちらも図を書いて整理するのは変わらないでしょう。
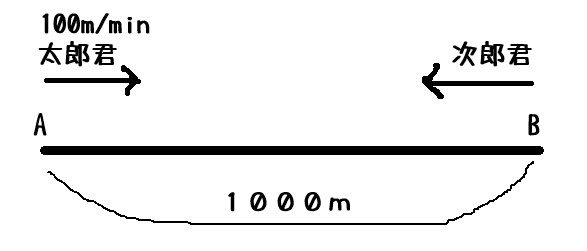
太郎君と次郎君が反対向きに歩いているので、二人の速さを足した速さで二人が近づく事が分かります。
1000mを4分ですから 250m/min です。
太郎君の速さ+次郎君の速さ=250m/min になりますから
次郎君の速さは150m/min です。
数学的解法
算数と同様に図を書いて整理します。
次郎君の速さをXとおく。
4×100 + 4X=1000
X=150
よって 次郎君は150m/min で歩いている。
速さ系の問題は 比で解く事も多く、算数も数学も処理方法は殆ど変わらないように思います。
1△、1□のように記号で比を置くか、XとYを使うかの違い程度でしょうか。
旅人算②
少し応用的な旅人算です。
灘中学2020年度 1日目 大問3 より引用
図のように,4地点A,B,C,Dを結ぶ直線の道路があります。BとCは84m,CとDは1260m離れています。
最初,太郎さんはA,次郎さんはCにいます。2人がBに向かって同時に歩き始めると,同時にBに到着します。
また,最初の状態から2人がDに向かって同時に歩き始めると,同時にDに到着します。
このとき,AとBは□m離れています。ただし,Bに向かうとき,Dに向かうときで太郎さんの歩く速さは同じです。また,次郎さんも,Bに向かうとき,Dに向かうときとで歩く速さは同じです。
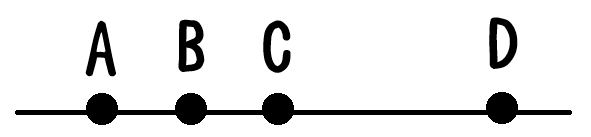
引用終わり
算数的解法
図に色々と書き込みます。
これは数学を用いる時も同じです。
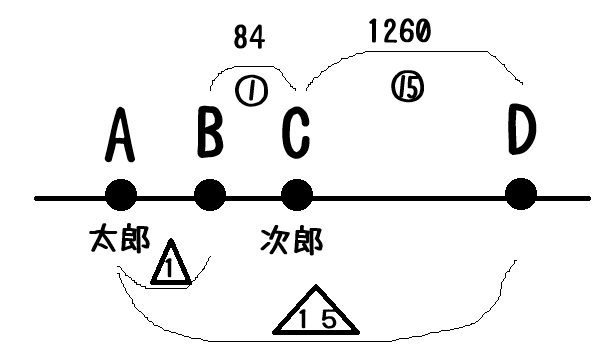
B-C間を次郎君が進む距離 84mを①とすれば CD間は 1260/84=⑮です。
速度一定だから、距離の比=かかる時間の比です。
よって太郎君がA-B間を進む時間を1△とすればAーD間は15△です。
太郎君も速さ一定ですから 距離の比も1△:15△です。
よってBーD間は14△ですから、(1260+84)/14=96=1△
A-B間は1△ですから、答えは96m です。
数学的解法
この手の問題は算数も数学も殆ど変わりません。
文字式で整理するとすれば
A-B間をX とすれば 次郎君のかかった時間の比1:15から
A-B間=X A-D間=15X
よってB-D間=14X
1260+84= 14X
X=96
よって A-B間は96m
流水算
流水算などと名前がついていますが、旅人算とやっている事は殆ど同じです。
水の流れの向きによる速度の増減を考慮するだけです。
【問題】
同じ川にA点とそこからいくらか離れたB点があります。
A点は上流に位置し、B点に向かって川の水が一定の速度で流れているものとします。
船MがA点からB点へ下るのに6時間,上るのに8時間かかりました。
船NはA地点からB地点へ下るのに12時間かかりました。
船NはB地点からA地点へ上るのに何時間かかるでしょうか?
算数的解法
旅人算と同じように図を書いて整理します。図は割愛。
速度は時間の逆比になりますから
船Mは 上り時 ⑥ 下り時 ⑧ 差は②です。
上り時には川の流れが邪魔をし、下り時には助けてくれますから、川の流速の2倍分船の速度に差が付きます。
よって、川の流速は①です。
船Mと船Nの下り時の速度を比較すると
6時間と12時間ですから 船M下り:船N下り=2:1です。
よって 船Nの下り速度を比で表すと ⑧÷2=④ 流速による上り下りの差は②ですから 船Nの上り速度は②です。
速度比は 船N上り:船N下り=②:④=①:②
時間は逆比になりますから ②:①です。
よって上りにかかった時間は 12×2=24時間です。
比で解くのが普通は早いでしょう。
数学的解法
旅人算同様 特に違いはありません。
①、②などではなく、X,Yの文字式で比を整理する程度です。
流水算(難関レベル)
灘中学2017 1日目 大問5より引用
一定の速さで流れる川でボートをこぎます。静水でボートが進む速さは一定です。
ある地点Aでボールを川の下流に流すと同時に上流に向かってボートをこぎ始めました。
そして,地点Aから上流に300mのところでボートを川岸につなぎとめて10分間休んだのち,下流に向かってこぎました。
すると,地点Aから下流に1030mのところでボールに追いつきました。
下流に向かってこいだ時間は,上流に向かってこいだ時間より4分長くかかりました。
このとき,静水でボートが進む速さは川の流れの速さの[①]倍で,川の流れの速さは毎分[②]mです。
引用終わり
算数的解法
割愛しますが、複雑なダイアグラムを書き、等しい距離に注目して解き進める形になります。
中々にセンスが問われる作業になります。
希望があれば詳細を書きますが、中々面倒な作業になります。
この手の問題は数学的にシステマチックに解いた方が楽だと思います。
グーグルで検索するといくつか算数解法の解説ページがヒットしましたので、それを見て頂いても良いかと。
数学的解法
素直に立式していきます。
静水時のボートの速さをXとおく
流速をYとおく
地点Aから上流300mまでにかかった時間をtとする。
未知数が3つだから3つ立式すれば良い。都合よく3つ立式出来るように問題文が組まれている。
上流までの関係式
(X – Y)t=300‥‥①
下流までの関係式
(X + Y)(t+4)=1330‥‥②
ボールの関係式
Y(t+10+t+4)=2Yt + 14Y = 1030‥‥③
連立していきます。
②-①を計算すると…
⇒2Yt + 4X + 4Y =1030‥‥④
④の1030に③を代入すると…
2Yt + 4X + 4Y = 2Yt+14Y
移行して計算すれば
4X = 10 Y を得る。両辺を2で割り
2X = 5Y
よって X:Y=5:2
① 5/2 倍
川の流れの速さが知りたいので Y以外の文字を消せば良い。
X=5/2Y を利用し①に代入
3/2Yt=300
Yt=200‥‥⑤
同様に②に代入
7/2Y(t+4)=1330
7/2Yt + 14Y=1330‥‥⑥
⑤を⑥に代入すると
700+14Y=1330
14Y=630
630/14==45=Y
よって Y=45m/min
整数、公約数など(難関レベル)①
灘中学2018年度 1日目 大問4 より引用
3を8個かけてできる数3×3×3×3×3×3×3×3,すなわち6561の約数のうち,4で割ると1余るものは,1を含めて全部で(①)個あります。また,30を8個かけてできる数30×30×30×30×30×30×30×30の約数のうち,4で割ると1余るものは,1を含めて全部で(②)個あります。
引用終わり
算数的解法
表を書いて整理します。
『算数的』と言っておりますが、数学で同様の問題が出た場合も表を書いて整理する事は有効です。
約数は場合の数で表現出来ますから
約数は 3^0 ~ 3^8 の9個
1、3、9、27、81、243、‥・・・6561
4で割った余りをそれぞれ順番に並べると‥‥
1、3、1、3、1、3、・・・・・ どうやら 3と1が交互に並ぶらしい。
念の為6561も3で割ってみると 余り1 よって約数9個のそれぞれの余りは
1,3,1,3,1,3,1,3,1
よって①=5個
30=2×3×5
30^8=2^8×3^8×5^8
だから場合の数で約数の数は 9×9×9=729個
正直なところ、初見で余りの性質を全く知らない状態でこの問題を解くのは難しいでしょう。
実験的に求めるならば
色々と試してみる。
2^0× 3^0 × 5^0=1 は 4で割ると余り1
2^1 × 3^0 × 5^0=2 は 4で割ると余り2
2^2 × 3^0 × 5^0=4 は 4で割ると余り0
2^3 × 3^0 × 5^0=8 は 4で割ると余り0
なるほど。2^2以上は全部割り切れちゃうから使えないんだな‥‥。
2^0 × 3^0 × 5^0=1 は 4で割ると余り1
2^0 × 3^0 × 5^1=5 は 4で割ると余り1
2^0 × 3^0 × 5^2=25 は 4で割ると余り1
2^0 × 3^0 × 5^3=125 は 4で割ると余り1
どうやら5が何乗になっても余りは変わらないらしい。
3はさっきやった通り、1、3、1、3が交互に続く‥‥
3と5の結果を考えると多分余りが1同士をかけてもどうやら余りは1らしい。
(1)が誘導のはずだし、余りが1になるものだけが使えると考えれば…‥
2は 2^0だけが使える。
3は5個だけ使える。
5は全部使える。
だから 1×5×9=45個!!
答えは45個! ②=45個
数学的解法
合同式を使えば容易です。
3≡-1(mod4)
ゆえに 3^n (n=0,1,2,3,4‥‥) 1、-1、1、-1‥‥と続くから ①=5個
30^8 = 2^8×3^8×5^8
i,j,kを0~8の整数とおく
2^i×3^j×5^k ≡1 (mod4)になるものを探せば良い
恐らく全て ≡1(mod4)の時しかなさそう。
2^0≡1(mod4)
2^1≡2(mod4)
2^2≡0(mod4) 以降は全て≡0だから 1通り
3は①より 5通り
5^0≡1(mod4)
5^1≡1(mod4) 以降は全て1
ゆえに 5は9通り
よって 1×5×9 =45通り。 ②=45個
整数、公約数など(難関レベル)②
灘中学2018年度 1日目 大問4 より引用
2以上の整数Aに対して,Aの約数をすべてかけあわせてできる数を[A]と書きます。例えば,[6]=1×2×3×6=36です。
B=6のとき[2×B]/[B]=①です。また,[2×C]/[C]=192となる2以上の整数Cは②です。
引用終わり
算数的解法
まずは①を解いてみます。この手の問題は殆ど確実に①が②の誘導なので、そこを意識しながら法則を探します。
[12]=1×2×3×4×6×12
[12]/[6]=(1×2×3×4×6×12)/(1×2×3×6)
約分すれば 4と12だけが残るので 答えは4×12=48 ①=48
この残った数の4と12は何だろう?素因数分解してみよう。
4=2^2
12=2^2×3
あぁなるほど 2×Bで2の素因数が一つ増えたから 2^2の分の約数が増えたんだな。
だから 最初の数が 2^3×5 だったら 2Bは 2^4 ×5 になるから、2^4系列の約数だけが残るんだな。
①の答えの48を素因数分解してみよう。
48=2^4×3
あぁそうか。2^2系列の約数が二つ残ってるから、2^2が二つで 2^2×2^2 = 2^4になるんだな。
よし、192を素因数分解してみよう。
192=2^6×3
素因数が二つだから きっと[2C]/[C]で 2^3×3^0 と 2^3^×3^1が残ったんだな。
だからCは2^3から2を一つとって 2^2×3のはずだから・・・・・
答えは C=2^2×3=12
②=12だ!!
数学的解法
約数の積 [6]=1×2×3×6=36
は 約数の個数を n個とすれば 6^(n/2) になります。
Bと2Bでは 素因数の数が 2^1の分一つだけ異なります。
6=2×3 で約数は4個です。
12=2^2×3で約数は6個です。
ゆえに 12^3/6^2=48 ①=48
192を素因数分解すると2^6×3です。
素因数の種類が二つしかなく、かつ3の次数が1のため、2^1が掛けられた際に増える約数は 2^a ×3^0 と 2^a × 3^1の二つのみ です。
よって 2^(2a)=2^6 a=3
Cは 2^(a-1)×3になりますから
2^2×3=12
よって②は12
これは 素因数の種類が二つだけなので簡単です。
試しに C = 57600 =2^8×3^2×5^2 で解いてみましょう。
この時点で 答えは 2^a×3^b×5^c の形になる事が確定します。
2^1増えた分、3^(0~b) と5^(0~c)分の約数が増えたはずです。
その総積が3^2 と5^2 ですから b=1,c=1が確定します。
また、この結果から約数は4個増えたという事ですから、2^a が4つ掛けられたはずです。
よって 2^(a×4)=2^8
ゆえに a=2
C= 2^(a-1)×3^1×5^1 ですから
答えは 2 ×3 ×5 =30 です。 ②=30
整数、公約数など(難関レベル)③
灘中学2002年1日目 大問3より引用
連続した5つの整数の積が2441880であるとき、これら5つの整数のうち最も小さい整数は□である。
引用終わり
算数的解法
何となくあたりを付けてみる。
10×10×10×10×10=100,000<2,441,880
だいぶ小さいけど100だと大き過ぎる。
20だと 2倍が5個で32倍のはずだから
100,000×32=3,200,000>2,441,880
だから 20前後の数になりそうだな‥‥。
作問者は素因数分解をしてあたりをつける方法を推奨しているように思います。
因数分解すると 23×33×5×7×17×19 になります。
ここから17と19は必ずあると分かるので、計算して確認する‥‥‥ よりも‥‥
中学受験生は計算力の高い子が多いので、この手の問題は悩むより計算した方が多分早いです。
そろばんをやっている子ならば一瞬でしょう。
15×16×17×18×19=1,395,360
16×17×18×19×20=1,860,480
17×18×19×20×21=2,441,880
よって 答えは17
数学的解法
ただの計算問題ですから、少し工夫をする程度ですね。
素因数分解をするのが基本です。
5個の連続する整数の積は5 !=120 の倍数ですから
2,441,880/120=20349
各位の和が9の倍数ですから9で割れそうです。
20349/9=2261
2261は割と有名な数字です。7×17×19です。
知らなければここで苦戦しそうですね。
苦戦した場合は 算数的解法で述べた 『大体20周辺だろう』という事実から19あたりで割ってみる事が出来るかと思います。
素因数分解(素因数ではないが)の結果は以下のようです。
120×9×7×17×19=2^3×3^3×5×7×17×19
17と19が5個の整数のうちの二つなのは確定です。
18も確定ですから 2×3^2=18
残りは2^2×3×5×7 で二つの数字を作れば良い。
2^2×5 と 3×7 で良さそうです。
よって 17×18×19×20×21
答えは17です。
ただの計算問題ですから、どちらかと言えば算数よりの解法となります。
仕事算(基本)
Aさんは仕事の処理に6日かかります。
Bさんは同じ仕事の処理に12日かかります。
AさんとBさんが協力して仕事を処理した場合、何日で仕事は終わりますか?
算数的解法
仕事の総量を1とします。
Aさんは 1/6
Bさんは 1/12
仕事をすると考える。
A+B=2/12 + 1/12 =3/12=1/4
AさんとBさんが二人で仕事をすると 1/4/日ずつ処理出来ます。
よって 4日間
数学的解法
仕事の総量をXとする。
Aさんの一日当たりの仕事量は 1/6×X
Bさんの一日当たりの仕事量は 1/12×X
A+Bさんの仕事量は (1/6 + 1/12)X =1/4×X
よって4日間
殆ど同じです。1と置くかXと置くかの違いだけです。
仕事算(難関レベル)
灘中学2022年 1日目 大問2より引用
ある仕事に兄と弟が取り組みます。兄は30分働くごとに5分休むことを繰り返します。弟は働き始めると休まずに働き続けます。兄は働き始め,その95分後に弟も一緒に働き始めると,兄が働き始めてから135分後にこの仕事が終わります。また,弟が働き始め,その90分後に兄も一緒に働き始めると,弟が働き始めてから140分後にこの仕事が終わります。この仕事を弟だけで終わらせるには□分かかります。
引用終わり
算数的解法
□第一条件
兄が135分 弟が135-95=40分 働くと仕事は終わる
ただし、兄は5分×3の休憩をしているので実質120分
よって 仕事の総量=兄120分+弟40分
□第二条件
弟が140分 兄が50分 働くと仕事は終わる。
ただし、兄は5分×1の休憩をしているので実質45分
よって 仕事の総量=兄45分+弟140分
二つの条件を見比べると 弟100分=兄75分のようです。
仕事の処理速度を比で表すと 兄:弟=4:3です。
兄が120分かかる仕事は弟は 120×(4/3)= 160分かかります。
よって第一条件より 仕事の総量 = 弟160分+弟40分=弟200分
よって答えは200分
数学的解法
□第一条件
兄が135分 弟が135-95=40分 働くと仕事は終わる
ただし、兄は5分×3の休憩をしているので実質120分
仕事の総量をK 兄の毎分仕事量をX 弟の毎分仕事量をYとすれば
K=120X+40Y‥‥①
□第二条件
弟が140分 兄が50分 働くと仕事は終わる。
ただし、兄は5分×1の休憩をしているので実質45分
K=45X+140Y‥‥②
①式に②を代入すれば
120X+40Y=45X+140Y
75X=100Y
3X=4Y‥‥③
①に③を代入すれば
K=160Y+40Y=200Y
よって答えは200分
仕事算、ニュートン算は代数処理が容易な場合が殆どですので、数学的に解いた方が間違いにくいように思います。
ニュートン算(基本)
典型的な牧場問題です。
Sharari牧場では 牛を24頭放牧すると16日で草がなくなります。
36頭の牛を放牧すると8日で草がなくなります。
では60頭の牛を放牧した場合、草は何日でなくなるでしょうか?
ただし、草は一日ごとに一定の割合で生えてくるものとします。
算数的解法
□第一条件
一日に生えてくる草を 1△とします。
牛一頭が一日で食べる草を1□とします。
24頭が16日間食べ続けたので 16×24□=384□です。
その間に生えてきた草は1△×16=16△です。
よって、元から生えていた草は 384□ー16△ です。
□第二条件
36頭が8日間食べ続けたので 牛が食べた量は 8×36□=288□です。
その間に生えてきた草は1△×8=8△です。
よって、元から生えていた草は 288□-8△です。
二つの条件を見比べると
384□-16△と288□-8△がイコールだという事に気付きます。
だから
384□-288□と16△-8△が同じだと分かります。
よって 96□=8△
△=12□
元から生えていた草は 288□ー8△だから
288□ー96□=192□
60頭の場合、一日で食べる量は60□、一日に生えてくる草は12□だから
一日に減る草の量は 60□ー12□=48□
元から生えていた草 192□ を 48□で割れば
192□÷48□=4
よって答えは 4日間
数学的解法
違いは△、□の代わりにX,Yなどの記号を使うくらいです。
元から生えている草の量を K
牛一頭が一日に食べる草の量を X
一日に生えてくる草の量を Y
とおく。
□第一条件
K=16(24XーY)‥‥①
□第二条件
K=8(36XーY)‥‥②
①に②を代入すると
8(36XーY)=16(24XーY)
両辺を8で割り、展開すれば
36XーY=48Xー2Y
Y=12X‥‥③
①に③を代入すると
K=16(24Xー12X)
K=192X
□60頭の場合
1日当たりの草消費量は③より
60X-12X=48X
よって
192X/48X=4
よって4日間
基本的に算数も数学もやっている事は同じです。
数学的に処理した方が見やすく、間違いも少ないように思いますが如何でしょうか?
間違えやすい線分図を書く必要も殆どありません。
ニュートン算(難関レベル)
桜蔭中学 2012年 入学試験より引用
ある学校では,文化祭を2日間おこないました。2日とも,入場開始前の受付にすでに長い列ができていて,入場開始後は5分ごとに100人の入場希望者が列に加わっていきました。1日目は受付を7ヶ所にしたところ,入場開始から45分後の列の人数は10人になりました。2日目は入場開始前の列が1日目よりも25人多かったので,受付を8ヶ所にしたところ,入場開始からちょうど20分後に並んでいる人がいなくなりました。
どの受付でも,5分ごとに受付できる人数は同じです。
(1)1ヶ所の受付で,5分ごとに何人の受付ができますか。
(2)2日目の入場開始前に列に並んでいた人は何人ですか。
引用終わり
算数も数学も似たようなものなので数学的解法のみ
数学的解法
1日目に並んでいた人数をK
受付1ヶ所あたりの5分毎の処理人数をX
とおく。
□第一条件
5分毎に100人増えるので45分で
9×100=900人
45分後に10人処理しきれていなかったので
K+900-10=9X×7
K+890=63X‥‥①
□第二条件
5分毎に100人増えるので20分で
4×100=400人
20分で処理しきったので
K+25+400=4X×8
K+425=32X‥‥②
①ー②で連立すれば
465=31X
X=15
よって(1)の答えは15人
①にX=15を代入すれば
K+890=63×15
K=945-890=55
二日目に並んでいた数は K+25だから
55+25=80
(2)の答えは80人です。
算数的に△□などを使って表現すると混乱し、計算ミスをしそうな問題です。
つづく
さて、少々忙しいため本日はここまで。
また後日加筆修正致します。
 Sharari-man
Sharari-man基本的に算数 or 数学 と明確に区分けしていません。
効率良く計算するために考え、立式するという手法を採用しています。
 Sharari-man
Sharari-man算数の問題と明確に区分けしている点としては
算数は厳密性が低くても答えがあっていれば良い というものです。
数学はそれが全ての整数において正しいか?といった厳密性を問うため、一般化が重要になります。
 Sharari-man
Sharari-man算数道場における、中学受験算数の学習目的は予習シリーズなどから『効率良く計算する手法や考え方』を学び取り、それを数学的にきっちりと立式し、解く力を養う事です。
 Sharari-man
Sharari-man灘中学などの問題は 大学入試レベルの内容を算数でも解けるように落とし込んだものが多くみられます。
この場合においては、大学入試レベルで必要な内容もあわせて指導しています。
例えば一般項の求め方や漸化式の立て方などです。
 Sharari-man
Sharari-manこのように明確に受験算数 or 数学を区分けせず、楽しく自由に学んでいるという感じです。
我が家の学習事例が少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。
ではまた!

コメント【コメント非公開、メールでの返信を御希望される方はその旨をご記入下さい】
コメント一覧 (2件)
Sharari-man様
こんにちは。いつも楽しい記事を有難うございます。算数、数学の記事は大好きで、楽しさがより一層増します。
追記の灘中学の入試問題の数学的解答、お見事ですね。こういった丁寧な解法が本来望ましいと思いますが、それは大学入試に任せて、中学入試では問いの急所的な核心部分を瞬発力に見抜く反射神経、センスを見ているのでしょうか?中学入試はSharari-man様ご指摘のように答えが得られればよい、ものであるため、緻密性が問われないのであるとしたら、クイズの解答のようなもののように思います。やはり、Sharari-man様がお示ししたような細部にまで行き届いたような解答ができるように、こどもたちは育ってほしいな、と思います。また続きを楽しみに致します。
ぞうさん様
Sharari-manで御座います。
いつもコメントありがとう御座います。
>中学入試では問いの急所的な核心部分を瞬発力に見抜く反射神経、センスを見ているのでしょうか?
初等幾何に関する問題は特にそのような傾向が強い気がします。
とはいえ、初等幾何も訓練によって灘中の問題を解けるレベルに習熟可能ではあると考えております。
正直なところ、△□などの記号を用いるよりも、指数、対数、代数を指導して理解してもらう方が、**算などの受験算数を教えるより合理的で理解もしやすいように感じています。
『受験算数』がちょっと特別視され過ぎている印象を持っています。
もう少し自由に子供達が学べる環境が整ってくると良いのですが。
またお気軽にコメントを頂けましたら大変嬉しく思います。
我が家の学習事例が少しでもぞうさん様の御参考になりましたら望外の喜びです。
ではまた!