公立カリキュラム先取り学習法のススメ

さて、表題の件です。
本記事はぴったりトレーニングを含む教科書レベルの参考書兼問題集の良いところを紹介するものです。

基本カリキュラム

算数道場では　中学受験の予定が無いお子様は

• 教科書ぴったりトレーニングを中学３年まで
• 初めから始める数学シリーズ　or 　はじめよう高校数学シリーズで高校３年基礎まで
• 青チャートを用いて入試基礎～標準レベルまで。
• プラチカ・１対１演習などを用いて入試応用レベルまで。

のルートで学習を進めています。
教科書ぴったりトレーニング中学３年生が終わった頃から中学受験算数も並行して進めています。

指導者側のメリット

• 指導者の学力への依存度が低い事
• 指導者の工数負担が少ない

が挙げられます。

学習初期に　1人でどうやって進めれば良いか　をしっかり指導すれば基本的に子供だけで進められます。
※多少の解説は必要ですが、解説が丁寧ですから解説に沿って親も指導しやすい。
※別途、漢字と語彙の学習は必要です。さすがに字が読めないと厳しい。

もし進められない場合は恐らく　１人でどうやって進めれば良いか　の指導が不足しています。

高校数学に入ると苦労する事もあるかもしれませんが、つまずいた単元に詳しい参考書を適宜与えてやれば充分に独学で進められるはずです。

指導者と学習者の両方に対するメリット

①公立カリキュラムに沿っており公立範囲の学習モレが無い

幾何や統計などに関する言葉の定義もしっかり学べます。言葉の定義がしっかりしてくれば、解答の解説や大人の説明も理解出来るようになります。

②難問が無く、解説が丁寧なので誰でも進めやすい

例えば小学５年生の算数は５年生だから、１０歳だから理解出来るという訳では無いと考えております。
理解出来る理由は大変シンプルで　小学４年生までの算数と漢字と語彙を理解している　からです。

これを遡っていくと、
小３は小２までを理解しているから。
小２は小１までを理解しているから。
このようになります。

よって教科書ぴったりトレーニングを現学年から順番に進めていきつつ、並行して計算補助教材や漢字と語彙力の学習をすれば、多くの方が中学３年まで進められると考えています。

漢字と語彙は高いレベルまで学ぶ必要はありません。
中学３年の数学まで進めるために必要なレベルとしては

小６までの漢字が読める
ふくしま式レベルの文法基礎が分かる

程度で充分です。

③指導者の数学的な説明を理解出来るようになる

これも大きなメリットだと考えています。。
算数道場では算数の難問を解説する時に以下のように説明する場合があります。

このような数学を用いた会話が成り立ちます。するとかなり学習効率が向上すると考えています。

指導者側も楽ですし、子供の理解も早いように思います。

本学習法のデメリット

現在のところデメリットは殆ど無いと考えておりますが、無理やり挙げてみましょう。

①中学受験には対応出来ない

例えば中学３年までの数学を完璧に理解していても、難関中学の入試には対応出来ません。
中学入試算数の方が圧倒的に難しいです。

ただし、勘違いしないで頂きたいのは、中学３年までの数学学習は中学受験算数を解くために確実に役立つという点です。学習した内容が無駄になる事は全くありません。

⓶進みが緩やかなので要領の良いお子様には合わない

かなり丁寧にスモールステップで進むため、進捗は緩やかです。
要領が良く、どんどん進められるお子様にとってはやや進捗が緩やか過ぎると感じるかもしれません。

具体的な進捗速度は以下の記事を御参照下さい。我が家の実績値です。

【参考情報】
中学受験算数はかなり難しいです。
以下のリンクから試読可能な問題集を見て頂ければ分かりますが、方程式や素因数分解を使わないと解くのが困難な問題が多いです。特殊算と称しておりますが、実質は中学範囲の知識を利用している事と同義です。

Sharari-manの　主観で　ぴたトレとトップクラスの難易度を比較　すると以下の図のようです。

ぴたトレ中３　＜　トップクラス４年　は道場や息子の実績から間違いありません。
トップクラス3年の時点で公立小6より難しいと思います。

指導者としての下準備について

先に結論を言いますと

参考ですが　Sharari-manの場合は相当量の学習を積んでから指導を開始しました。

受験算数

予習シリーズ5〜6年一式
過去問演習
灘中、甲陽、東大寺、西大和、洛星、洛南、開成、築駒、駒場東邦、渋幕をそれぞれ５～10年分

中学数学

塾技中学
中学数学は大阪公立Ｃ問題、灘高、開成高、洛南高を10年分

高校数学

センター入試過去問　5年分
名大、京大、東大、東工大の2次試験を5～10年分

大学受験演習は頭の回転も遅くなっており非常に苦労しました。
例えば東大だと150分間集中し続ける必要があります。
老体にとって夜なべして過去問演習を進めるのはかなりきつかったように思います。

さて、この程度の事前学習をしておけば子供達から聞かれても答えられない事は殆ど無くなります。
しかしながら多くの工数が発生しますから、全員が出来る訳ではありません。

社会人でここまで学習出来る工数がある方は少ないと思います。
Sharari-manは１日3～4時間睡眠で生存可能なショートスリーパーですから、充分に工数を確保する事が出来ました。

なぜ私がこの下準備をしたかと申しますと、どの学習ルートでも指導出来るようにしたかったからです。
大切なお子様を預かり指導する以上、最大限努力しなければならないという責任感もありました。

さて、当然ながら指導者がつきっきりで横で教えながら　難易度の高い問題集を進めた方が　進捗は早くなる傾向があるように思います。
専属の家庭教師が付いているのと同義ですからね。
しかしながら、全ての親御様がそれに対応出来るかと言えば、そうではありません。

• 学力的に厳しい方
• 仕事で指導するための工数が無い方
• 教えるのが苦手な方

色々な事情で難問の指導が出来ないケースがあるかと思います。
上記に当てはまり

と思われた方は　教科書レベルの問題集を進めるルートの方が少ない負担でストレスも少なく進められると思います。

今は中学受験ブームです。

• 自分の学力で教えられるのか？
• 工数は充分に確保できるのか？

などの自己分析が出来ていないまま、トップクラス問題集などの難しい割に解説が簡素な問題集にチャレンジして、撃沈された方も多いのでは無いかと思います。

以下の記事でも言及致しましたが、難易度が高い割に解説が簡素な問題集に取り組んで

という状況の方も多いのではないかと思います。

そのような方は公立カリキュラムに沿った先取り学習を進めた方が、楽しく和気あいあいと進められるのでは無いかと思います。
解説はこれ以上は無いレベルで丁寧ですから、もし指導者側が算数／数学が苦手だったとしても共に学びながら進められると思います。

公立学習ルートと中学受験算数

• 公立ルートの中学数学まで進めば、基礎レベルの受験算数は解けます。
• 公立ルートの高校数学まで進めば、中堅中学の算数は解けます。
• 高校数学の習熟が深まると共に中堅～難関中学の算数は解けるようになります。

また中学受験をしない場合においては

高校数学の先取りが一通り終わった状態で　中学に入学する訳ですから、入学後に余裕があります。
小学生で高校数学まで進んでいれば、大学受験までに６年間ありますから、余裕を持って大学二次試験レベルの学習が進めれます。

小学生の間に中学数学までだけでも終わらせておけば、中学では部活動をしながらスキマ時間に高校数学の先取りをする程度でも良いと思います。

あくまでも・・・・・

という御提案です。

公立カリキュラムの速度

というのが　Sharari-man　の主張です。

学習速度のイメージとしては以下のようです。

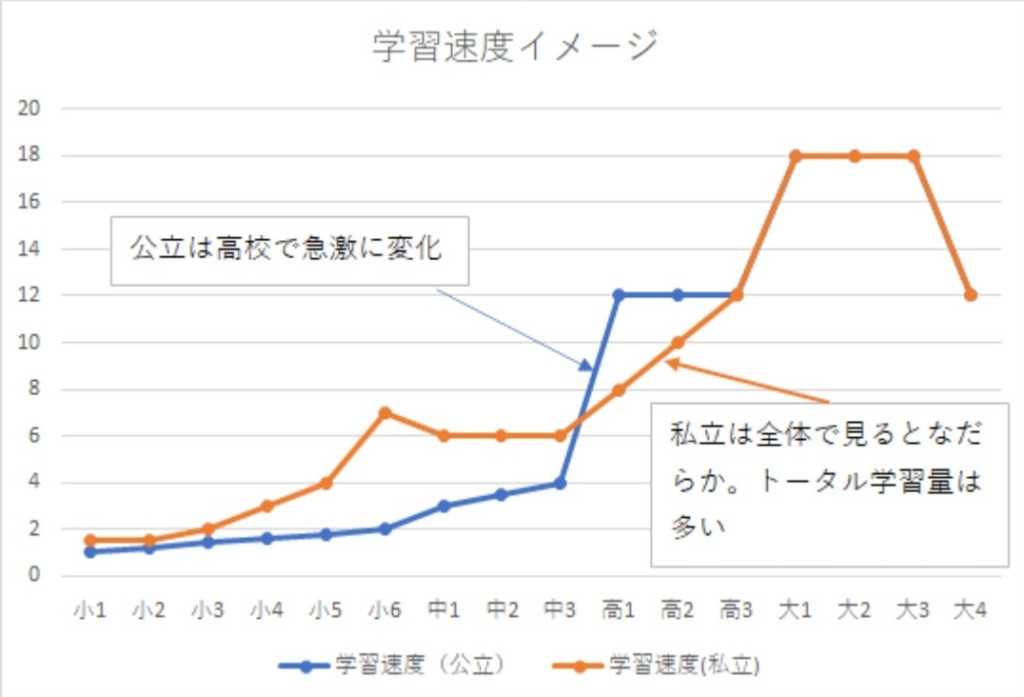
中学受験生は進捗が緩やかな小学生時代にかなりの学習量を積み、中学～高校では無理なカリキュラム学習をしていない事が分かると思います。

まとめ

• 解説が丁寧で指導者が指導しやすい。
• 指導者の事前学習が不要で工数負担が少ない
• 子供が一人で学び進めやすい
• 公立カリキュラムの高校時の厳しさを軽減出来る

ちなみにですが、近年の「大学入試　共通テスト」は中学受験風の問題が出題されています。
日本語の長文を読み、条件整理を行い、解くタイプの問題です。
恐らく難関私立中学出身のお子様は共通テストはそれほど苦にしないのではないかと思います。

我が家の学習事例が少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。

ではまた！