さて、表題の件です。
以前に運営していたブログの記事の焼き直しです。
難関大合格に関する問い合わせが幾つかありましたので、参考になればと思い焼き直しを致しました。
英語と数学の先取り学習を進めていれば大学受験に対してどの程度有利に働くのかを検証してみます。
難関大のモデルケースとして 東京大学と京都大学を採用しました。
検証① 配点と合格者最低点
東京大学と京都大学の 配点と合格者最低点
今のところMusukoは工学部志望なので東大は理系、京大は工学部で確認しました。
■東大 理系 配点

共通テストの英数の配点が 49点
二次試験の英数の配点が 240点
合計 289/550 (英数以外の配点261点)
英数で85%取れた場合の得点:245.65点
理科Ⅰ類 合格者最低点10年平均 326.3点
理科Ⅱ類 合格者最低点10年平均 316.1点
理科Ⅲ類 合格者最低点10年平均 383.8点
理科Ⅰ類の合格に必要な他科目の得点率 (326.3 – 245.65) ÷ 261×100 =30.9%
理科Ⅱ類の合格に必要な他科目の得点率 (316.1 – 245.65) ÷ 261×100 =27%
理科Ⅲ類の合格に必要な他科目の得点率 (383.8 – 245.65) ÷ 261×100 =52.9%
★京大 工学部 配点

共通テストの英数の配点が 50点
二次試験の英数の配点が 450点
合計 500/1000点 (英数以外の配点500点)
英数で85%取れた場合の得点:425点
工学部 合格者最低点10年平均 561.5点
工学部の合格に必要な他科目の得点率 (561.5 – 425) ÷ 500 ×100 =27.3%
まとめると 以下の事が言えます。
英語と数学で 85%の得点率を取る事が出来れば 他の科目の得点率は
東大理科Ⅰ類では 30.9%
東大理科Ⅱ類では 27%
東大理科Ⅲ類では 52.9%
京大工学部では 27.3%
で良い事が分かります。
英数の得点率毎の合格に必要な他教科の得点率は以下の通りです。
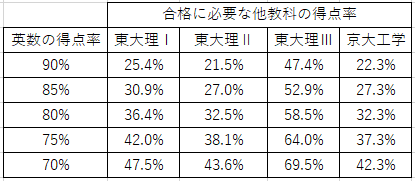
以上の事から 英数で8割前後取れれば、東大理Ⅲ以外は英数以外の教科は3~4割の得点率で良い事が分かります。
 Sharari-man
Sharari-man単純に配点だけを考えても
東大は 289/550 =52.5%
京大は 500/1000=50%
となっており、英数の得点だけで50% ですから、その影響の大きさが分かるというものです。
検証② 難易度
Sharari-man が 東大と京大 直近7年分の 数学と英語の過去問を制限時間有りで実施しました。
事前にかなりの量の演習を積んだ状態で挑んでおります。
数学は概ね8割~ 東大は4完は堅く、平均は5完半 たまに6完
数学は採点基準が不明なため、予備校の解答ベースで採点しましたが、かなり厳しめに見ても7割5分以上はあると思います。
英語も8割~(リスニングは音声データが無く未実施)
以上の事からSharari-manと同レベルの数学力と英語力があれば 80%の得点率は十分可能です。
参考としてSharari-manのスペックを紹介すると・・・・
数学 ⇒ 数学検定1級、大学は工学部、数学好き、仕事で数学を使う(解析メイン)
英語 ⇒ TOEIC850点~、英検準1級、仕事で英語を使う(海外論文、決算書、海外出張,打ち合わせ)
このようなスペックですが、正直なところ【学力】よりも問題形式慣れの方が寄与度が高いように感じます。
東大でしたら6問1セットで150分で解ききる訓練 が大変重要です。かなり時間が厳しいためです。
英語についても出題形式が例年概ね同じパターンですから、形式に慣れておく事は大変重要です。
必要な学力
もう少し客観的に能力の目安を提示すると以下のようです。
■数学
青チャートが完璧に理解出来ている
プラチカ、1対1、掌握などの難問が理解出来ている
過去問演習が終わり、問題形式に慣れている

■英語
英検1級、TOEIC850点 程度あれば充分に解く事が可能なレベルです。
※単語、文法のレベル
ただし、東大、京大英語は文章の内容自体が難解な事が多いです。
Sharari-manのような大人であれば理解出来ますが、受験生の子供達では完璧に理解するのは厳しいように思います。
TOEIC、TOEFLなどに取組むか英語論文、洋書などを読んでおくと有利に働くでしょう。
英数に必要な能力目安はこの程度だと考えて頂ければ良いでしょう。
 Sharari-man
Sharari-man東大は特に時間が大変厳しいのが特徴です。
英語も数学もかなりのペースで解き進めないと終わりません。
「高速で精度良く解く」という本番を想定した訓練が最も重要になるでしょう。
検証③ 必要工数
現在のMusukoの進捗から必要な学習工数を計算してみます。
数学
数学検定2級取得済み
(準1級も合格可能だが取得していない)
青チャートは一通り終え、中堅国立の過去問演習中
青チャートから始めると概ね以下のような所要時間になるかと思います。
青チャート・・・500~600時間(Musukoの実績もこれくらいです)
難関大レベル・・・200時間~
最難関 or 数学検定1級レベル・・・200時間~
合計 1000時間
Musukoの場合、後400時間も学習すれば数学は最難関レベルに達するであろうという予測です。
英語
英検3級レベルは単語,文法共に完璧な状態
英検準2級レベルの単語、文法は概ね理解出来ている状態
著名な英検学習本によれば英検1級取得までには以下の工数が必要なようです。
英検3級まで 100時間
英検3級~1級 1190時間(色々な文献の平均値)
合計 1290時間
Musukoの場合、概ね1000時間程度で1級レベルに達するであろうという予測です。
必要工数
数学の必要工数=400時間
英語の必要工数=1000時間
各大学の問題形式慣れ=100時間×2=200時間
合計すると 1600時間程度の学習工数があれば良いようです。
検証④ 持ち工数
現在、Musukoは小学5年生です。(2024年3月現在)
毎日2時間 家庭学習を進めたと仮定すれば
365×2×=730時間/年
中学3年までの4年間では
365×2×4=2920時間
高校3年までの7年間では
365×2×7=5110時間
となっておりますから、中学3年までには難関大の英数が解けるレベルに仕上がるのではないかと思います。
実際のところ学習というものは短期集中した方が定着率が高いと考えています。
10時間/日 を 3日間で30時間 学習するのと
2時間/日 を 15日間で30時間 学習するのでは前者の方が学習効率が高いでしょう。
高校3年生になってから猛勉強して合格する方が多いのはこのためだと考えております。
しかしながら、Sharari-manはコツコツ毎日やるスタイルが好きだし、その力を子供達に身に付けて欲しいと考えています。
『高校2年生まで怠惰に過ごし、高校3年生の1年間だけ一生懸命頑張り、大学に合格する』
このような成功体験を得るのはあまり良くないと考えています。それで良い、社会でもそれで通用すると考えてしまうからです。
社会人になってからも継続的に毎日学ぶ事が出来る能力が大変重要です。
学ぶ事は山のように、それこそ無限にありますからね。
『毎日継続的に短時間学び、必要な時に短期集中で長時間学ぶ』
このような学習スタイルが私の好みであり、理想的であると考えております。
さて、少し話が飛んでしまいました。
毎日コツコツ進める前提ですが、難関大学合格可能レベルには充分達する事が出来る持ち工数がある事が分かりました。
殆どの方が充分な持ち工数があると言って良いでしょう。
重要なのは長期間、毎日コツコツ学習を進められるかどうかです。
結論
英数で80%前後の得点率を取る事が出来れば、難関大学合格に必要な他教科の得点率は30~40%で良い。
ただし、東大理Ⅲは50%以上必要である。
以上の事から、英数に偏重した学習は大学受験対策として効果的であると言える。
また、英数で80%程度の得率を取るためにMusukoに必要な学習工数は1600時間と推定出来る。
小学5年~中学3年の間に1日2時間の学習を続ければ 2920時間の学習時間確保が出来る。
小学5年~高校3年の間に1日2時間の学習を続ければ 5110時間の学習時間確保が出来る。
以上の事から、Musukoが中学3年生までの間に 難関大に対応出来るレベルの数学力と英語力を身に付ける事は可能であると言える。
参考情報
難関中学受験生の学習時間を色々な媒体から調べると概ね
4年生:1~3時間/日
5年生:2~4時間/日
6年生:3~5時間/日
のようです。通塾時間を含めるともっと多いと思います。
中央値を取り、4年は2時間、5年は3時間、6年は4時間 で3年間の学習時間を計算すると
(2 + 3 +4 )×365日 = 3285時間 となります。
よって、上であげた小5終盤~中3の約4年間で2920時間という学習時間はそれほど無理をさせずに可能な時間である事が御理解頂けるでしょう。
実際のところ、長期休暇中はもう少し勉強しておりますからかなり工数に余裕があります。
余った時間は 国理社の学習に充てる予定です。また、理科や国語については小学範囲に拘らず、中学以上の範囲を織り交ぜ、最適化した上で指導する計画にしています。
 Sharari-man
Sharari-manちなみに、私自身が難関大出身でもありませんし、「やりたい事が出来る大学ならばどこでも良い」というスタンスです。
よって大学合格のための学習というよりは実践的な内容に通じる学習に今後も力を入れていく予定です。
 Sharari-man
Sharari-man例えば、機械設計、マーケティング、統計、マネジメントなどです。
 Sharari-man
Sharari-man学習を進める中で機械ではなく、生物・化学分野に興味を持てば、そちらの知見を深めれば良いでしょう。
私が機械系エンジニアだからといって、Musukoの進路を機械だけに縛り付ける気持ちはありません。
一方で機械系エンジニアゆえ、効率良く機械系の指導が出来るというメリットは存分に活かすつもりです。
あとがき
さて、かなり大味な検証となっておりますが、多少は参考になるのではないでしょうか?
現在の状況は各御家庭によって異なると思いますから、御家庭が置かれている状況に合わせて学習計画を立案するために活用して頂ければと思います。
 Okusama
Okusama難関大学に絶対合格しないとダメ!!!!!
 Sharari-man
Sharari-man可能でしたら、このようなマインドを持つ事はやめて頂きたいというのが本音です。
 Sharari-man
Sharari-man学びたい事が学べる大学、学校が本人にとって良い学校です。
難関大だけが全てではありません。
 Sharari-man
Sharari-manぜひ、お子様の『好き』という気持ちを伸ばし、育み『楽しい家庭学習』に取組んでみて下さいね。
我が家の学習事例が少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。
ではまた!

コメント【コメント非公開、メールでの返信を御希望される方はその旨をご記入下さい】