さて、算数道場で5年生に出題した基礎問題です。
基礎的な練習問題です。難易度は高くありませんから、是非解いてみて下さいね。
問題
(1)0から1000の整数のうち13で割り切れる数はいくつありますか?
(2)0から1000の整数のうち13で割ったときの余りを3で割ると割り切れる整数はいくつありますか?
(3)0から1000の整数をそれぞれ13で割ったときの余りを3で割りました。3で割った時の余りを全て足した数を答えなさい。
(4)0から1000の整数をそれぞれ13で割ったときの余りを11で割りました。11で割ったときの余りを7で割りました。7で割ったときの余りを5で割りました。5で割ったときの余りを3で割りました。3で割ったときの余りを2で割りました。2で割ったときの余りが1になる整数はいくつありますか?
解答
(1)0から1000の整数のうち13で割り切れる数はいくつありますか?
13の倍数はいくつありますか?と言い換えると分かり易いでしょう。
0は13で割り切れる と考えますから 0 の数をカウントし忘れないように注意が必要です。
また、この(1)で余りは 0~12を繰り返すのだという事に気付く事が重要です。
1000÷13=76余り12
よって76 + 1 =77個
(2)0から1000の整数のうち13で割ったときの余りを3で割ると割り切れる整数はいくつありますか?
(1)で0~12のセットが77個ある事に気付く事が出来れば簡単です。
0~12のセットの中で3で割ると余りが0になる数は 0、3、6、9、12の5個
よって 5×77=385個です。
(3)0から1000の整数をそれぞれ13で割ったときの余りを3で割りました。3で割ったときの余りを全て足した数を答えなさい。
0~12、13~25、26~38・・・・というセットで考えます。
13で割った余りを3で割ると
0÷13=0・・・0 0÷3=0・・・0
1÷13=0・・・1 1÷3=0・・・1
2÷13=0・・・2 2÷3=0・・・2
3÷13=0・・・3 3÷3=1・・・0
4÷13=0・・・4 4÷3=1・・・1
5÷13=0・・・5 5÷3=1・・・2
6÷13=0・・・6 6÷3=2・・・0
7÷13=0・・・7 7÷3=2・・・1
8÷13=0・・・8 8÷3=2・・・2
9÷13=0・・・9 9÷3=3・・・0
10÷13=0・・・10 10÷3=3・・・1
11÷13=0・・・11 11÷3=3・・・2
12÷13=0・・・12 12÷3=4・・・0
次のループへ
13÷13=1・・・0 0÷3=0・・・0
14÷13=1・・・1 1÷3=0・・・1
・・・・・
0~12のセットの余りを全て足し合わせると12になります。
それが、77セットありますから
12×77=924 が答えとなります。
(4)0から1000の整数をそれぞれ13で割ったときの余りを11で割りました。11で割ったときの余りを7で割りました。7で割ったときの余りを5で割りました。5で割ったときの余りを3で割りました。3で割ったときの余りを2で割りました。2で割ったときの余りが1になる整数はいくつありますか?
13で割った時の余りが1の数字は最後まで余りが1です。
同様に11で割った時、7で割った時、5で割った時、3で割った時、2で割った時の余りが1の数字は最後まで余り1になります。
つまり0~12のセットの中で 13、11、7、5、3、2で割り進めていった時に余りが1になる数を探せば良いという事になります。
0~12の数それぞれを順に割り進めていくのが効率が良いでしょう。
0は最初から最後まで0
1は最初から最後まで1
2は2で割りきれるから0
3は3で割りきれるから0
4は3で割ると余り1だから1
5は5で割りきれるから0
6は5で割ると余り1だから1
7は7で割り切れるから0
8は7で割ると余り1だから1
9は7で割ると余り2になって2で割ると余り0だから0
10は7で割ると余り3になって3で割ると余り0だから0
11は11で割り切れるから0
12は11で割ると余り1だから1
下の表のようになります。
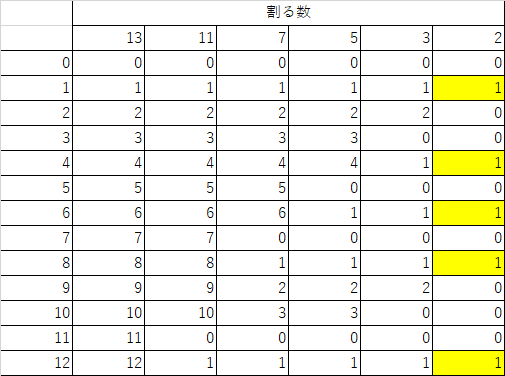
以上の事から 0~12のセットの中で1になるのは 1,4,6,8、12の5個
77セットありますから
5×77=385個
となります。
あとがき(学習の狙い)
さて、如何でしたでしょうか?
算数道場では4年~5年生くらいの基礎学習時にこのような問題を沢山解いてもらっています。
作問する事もありますし、過去問を改題する事もあります。
簡単な問題ですが、このような問題を数多く解く事で整数に対する理解が深まります。
学習の狙いとしては 整数の余りに関する法則、規則性と粘り強く検証する力を身に付けて欲しい というものです。
13で割った時の余り に着目させ、1も14も同じ関係性(法を13として合同)なんだという事に気付かせ、その後の合同式の学習に繋げるための予備学習です。
このような学習を通じて 整数と除算に対する理解を深め、ユークリッドの互除法やフェルマーの小定理や合同式の学習に繋げるようにしています。
互いに素などの用語やフェルマーの小定理などの各種定理についても 「小学生にはまだ早い」などと考えず、あの手この手を駆使して指導しています。
数学を先に学び進めていると、算数の問題を通じて より多くの事を学び取れると考えております。
これも数学の先取りをオススメしている理由です。
 Musuko
Musuko0÷13 って 割り切れる って言えるのかな?
割り切れる の定義は余り0 だから 割り切れるのか・・・?
 Musuko
Musukoという事は 偶数の定義は 2で割り切れる整数 だから 0は偶数なのか・・・?
 Sharari-man
Sharari-man整数問題に興味を持てば、自発的にこんな事も考えるでしょう。
興味の種を拾い集めて育てていけると良いですね。
さて、今後の受験を見据えると、整数問題、場合の数などは今のうちから習熟しておけば大学受験において大変有用です。
例えば灘中学の整数問題や場合の数は一橋大学の入試にあってもおかしくないような問題ですから、算数が得意な子供達はこの分野では随分有利です。
中学受験をしないお子様は 習熟に時間が必要な 四則計算、場合の数、微積計算などを少しずつ進めておくと良いと思います。
さて、公文式の良いところはこれらのうち、四則計算、微積計算をみっちり習熟させるところです。
両方とも習熟に時間がかかりますが、やればやるほど伸びる項目ですから、ここは公文式の大変優れた点だと考えております。
公文式は基礎的な内容定着と計算力向上には大変有用だと考えております。
地方で著名な塾が無い地域の方には公文式はオススメ出来る選択肢です。
少なくとも計算力向上は出来るからです。
案外、英語と国語の教材も優れております。
公文式に嫌悪感を示す方もいるようですが、食わず嫌いをせず一度覗きに行っても良いかと思います。
我が家の学習事例が少しでも家庭学習に取組む皆様の御参考になりましたら望外の喜びです。
ではまた!

コメント【コメント非公開、メールでの返信を御希望される方はその旨をご記入下さい】
コメント一覧 (2件)
Sharari-man様
こんにちは。九州出張お疲れ様です。いかがでしたか?
整数問題2連発、愚直に行いました。灘は見直しもしないといけないので時間がかかって仕方なく、受験現場では飛ばすかもしれません。Sharari-man様の別解は素晴らしいです。慣れていないと思いつきません。エンジニアの世界ではこういった考え方はよくあるのでしょうか。
Sharari-man様自作問題は誘導にのればよいので難問ではありませんが、数え間違えしそうです。こうやって問題はつくるものなのだなあ、と唸ってしまいました。
また楽しみにしております。
ぞうさん様
こんばんは。Sharari-manで御座います。
いつもコメントありがとう御座います。
顧客訪問、マーケティングのための九州巡回で御座いました。
TSMCの工場進出によって九州地方はやや景気が上向いており、求人も活況です。
アジア諸国との貿易に適した土地柄ですし、今後の更なる発展が期待されます。
子供達の学習環境としては 九州はラサールを筆頭にいわゆる管理型教育が多い事が特徴ですね。
塾も数社訪問させて頂きましたが、管理色がやや強めだと感じました。
九州地方には著名な進学校が多くあるため、著名な進学塾も多く存在します。ここは静岡県民としては羨ましく感じるポイントです。
この当たりの話は今後記事にしてみようかと思います。
さて、問題は楽しんで頂けたでしょうか?
灘中学の場合の数は良問が多く、Sharari-manはとても好きです。
n進数や除算(mod)は多少仕事で使いますね。
制御系の最適化を図る際にn進数で考えた方が良い場合があります。
modは分かり易いところでは モーターの位相(回転角度の現在位置)は総回転角度のmod360 で表されますから、自作でモーターの制御を組む際に使用したりします。
オリジナルの作問、過去問の改題を実施する場合は「何を学ばせたいのか?」が最も重要ですから、そこをスタート地点として考えます。
意外と楽しいものですし、ぞうさん様でしたら自作の作問が可能でしょうから、是非作問をしてお子様と一緒に楽しんでみて下さいませ!
いつも温かいコメントをありがとう御座います。大変励みになっております。
我が家の学習事例が少しでもぞうさん様の参考になりましたら望外の喜びです。
ではまた!